Giải Bài 7 trang 66 sách bài tập toán 7 - Chân trời sáng tạo - Bài tập cuối chương 8
Cho tam giác ABC có ba đường phân giác AD, BE, CF đồng quy tại I. Vẽ IH vuông góc với BC tại H. Chứng minh rằng \(\widehat {BIH} = \widehat {CI{\rm{D}}}\).
Sử dụng mối quan hệ giữa các góc trong tam giác để chứng minh
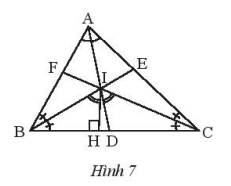
Ta có:
\(\widehat {DIC} = {180^o} - \widehat {AIC} = \widehat {IAC} + \widehat {IC{\rm{A}}} = \frac{{\widehat {{A^{}}} + \widehat C}}{2}\)
Ta có: \(\widehat {BIH} = {90^o} - \frac{{\widehat B}}{2} = \frac{{{{180}^o} - \widehat B}}{2} = \frac{{\widehat {{A^{}}} + \widehat C}}{2} = \widehat {DIC}\)
Suy ra: \(\widehat {BIH} = \widehat {CI{\rm{D}}}\)