
Hình sau mô tả một dụng cụ đo bề dày (nhỏ hơn 1cm) của số sản phẩm. Dụng cụ này gồm một thướng AC = 10 cm, có vạch chia đến 1 mm, gắn với một bản kim loại có cạnh thẳng AB sao cho khoảng cách BC = 1cm.
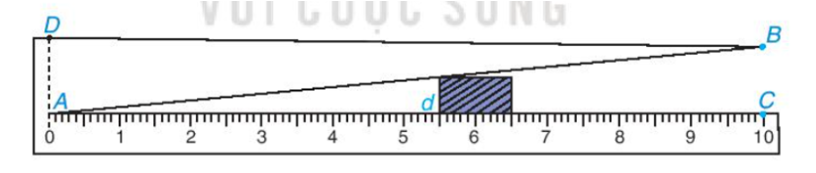
Muốn đo bề dày của vật, ta kẹp vật vào giữa bản kim loại và thước (đáy của vật áp vào bề mặt của thước AC). Khhi đó trên thước ta đọc đường "bề dày” d của vật (trên hình vẽ ta có d = 5,5mm). Hãy giả thích tại sao với dụng cụ đó, ta có thể đo được bề dày d của các vật (với d < 10 mm)

Sử dụng tính chất hai tam giác đồng dạng
Advertisements (Quảng cáo)

Kẹp vật vào giữa bản kim loại và thước như cách sử dụng đã mô tả; ta gọi B’C’ là đoạn ứng với bề dầy d cần đo của vât (nghĩa là d = B’C’). Dễ thấy B’C’ // BC vì cùng vuông góc với AC. Do đó $\Delta AB’C’\backsim \Delta ABC$, suy ra $\frac{B’C’}{BC}=\frac{A’C’}{AC}$.
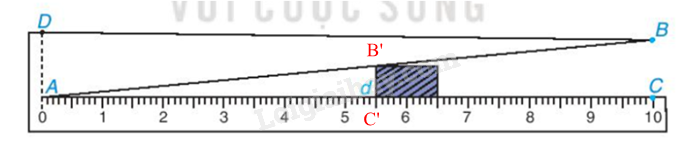
Do BC = 1 cm, AC = 10 cm nên đẳng thức này có nghĩa là B’C’ = $\frac{AC’}{10}$.
Vậy bề dày d của vật đúng bằng $\frac{1}{10}$ độ dài (cm) của AC’.
Chẳng hạn trên thức đo, AC’ = 5,5 cm có nghĩa là d = $\frac{5,5cm}{10}=5,5mm$.
