
Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm.
a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?
b) Tính khoảng cách từ giao điểm đó đến điểm C.

Sử dụng tính chất của hình bình hành và tia phân giác của một góc.

a) Vì AD > AB (5 cm > 3 cm) nên tia phân giác của góc A cắt cạnh BC.
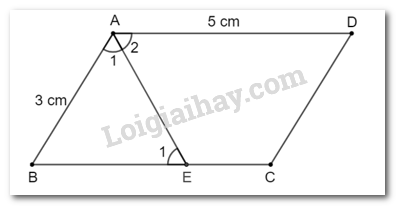
b) Gọi E là giao điểm của tia phân giác góc A với cạnh BC.
Advertisements (Quảng cáo)
Khoảng cách từ giao điểm đó đến điểm C tức là khoảng cách từ điểm E đến C, chính là độ dài đoạn EC.
Vì AE là tia phân giác của \(\widehat {BA{\rm{D}}}\) nên \(\widehat {{A_1}} = \widehat {{A_2}}\)
Vì AD // BC (vì tứ giác ABCD là hình bình hành) nên \(\widehat {{A_2}} = \widehat {{E_1}}\).
Do đó \(\widehat {{A_1}} = \widehat {{E_1}}\).
Tam giác ABE cân tại B (vì \(\widehat {{A_1}} = \widehat {{E_1}}\)) suy ra AB = BE.
Mà AD = BC (vì ABCD là hình bình hành).
Ta có BC = BE + EC.
Suy ra EC = BC – EC = 5 – 3 = 2 (cm).
Vậy EC = 2 cm.
