Chứng minh tứ giác AHCN là hình bình hành có \(\widehat {AHC} = {90^o}\) nên AHCN là hình chữ nhật Gợi ý giải bài 3.27 trang 66 SGK Toán 8 tập 1 - Kết nối tri thức Bài 13. Hình chữ nhật. Cho tam giác ABC, đường cao AH...
Cho tam giác ABC, đường cao AH. Gọi M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN. Chứng minh tứ giác AHCN là hình chữ nhật.
Chứng minh tứ giác AHCN là hình bình hành có \(\widehat {AHC} = {90^o}\) nên AHCN là hình chữ nhật
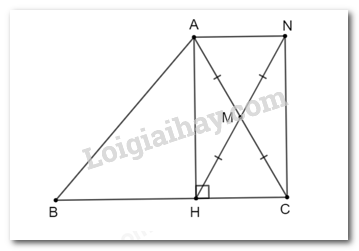
Theo đề bài, M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN.
Nên tứ giác ANCH có hai đường chéo AC và HN cắt nhau tại trung điểm M của mỗi đường.
Suy ra tứ giác ANCH là hình bình hành.
Hình bình hành ANCH có \(\widehat {AHC} = {90^o}\) nên tứ giác ANCH là hình chữ nhật.