Gọi Ou và Ov lần lượt là hai tia phân giác của hai góc kề bù xOy và x’Oy; A là một điểm khác O trên tia Ox. Gọi B và C là chân đường vuông góc hạ từ A lần lượt xuống đường thẳng chứa Ou và Ov. Hỏi tứ giác OBAC là hình gì? Vì sao?
Áp dụng tính chất tia phân giác của một góc và định lí tổng các góc trong một tứ giác.
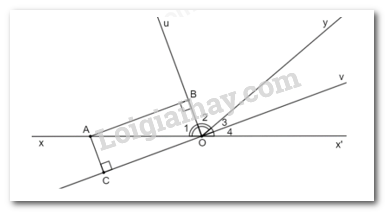
Vì Ou, Ov lần lượt là tia phân giác của \(\widehat {xOy};\widehat {x’Oy}\) nên \(\widehat {{O_1}} = \widehat {{O_2}};\widehat {{O_3}} = \widehat {{O_4}}\)
Mà \(\widehat {xOy} + \widehat {x’Oy} = {180^o}\) (vì \(\widehat {xOy};\widehat {x’Oy}\) là hai góc kề bù).
Hay \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} + \widehat {{O_4}} = {180^o}\)
Suy ra \(2\widehat {{O_2}} + 2\widehat {{O_3}} = {180^o}\)
Do đó \(\widehat {{O_2}} + \widehat {{O_3}} = {90^o}\) hay \(\widehat {uOv} = {90^o}\) suy ra \(\widehat {uOC} = {90^o}\) hay \(\widehat {BOC} = {90^o}\)
Vì B và C là chân đường vuông góc hạ từ A lần lượt xuống đường thẳng chứa Ou và Ov
Nên \(\widehat {ABO} = {90^o};\widehat {AC{\rm{O}}} = {90^o}\)
Tứ giác OBAC có \(\widehat {AC{\rm{O}}} + \widehat {BOC} + \widehat {ABO} + \widehat {BAC} = {360^o}\)
\({90^o} + {90^o} + {90^o} + \widehat {BAC} = {360^o}\)
270°+\(\widehat {BAC} = {360^o}\)
Suy ra \(\widehat {BAC}\)=360°−270°=90o
Xét tứ giác OBAC có \(\widehat {BOC} = {90^o};\widehat {ABO} = {90^o};\widehat {AC{\rm{O}}} = {90^o}\)
Vậy tứ giác OBAC là hình chữ nhật.