
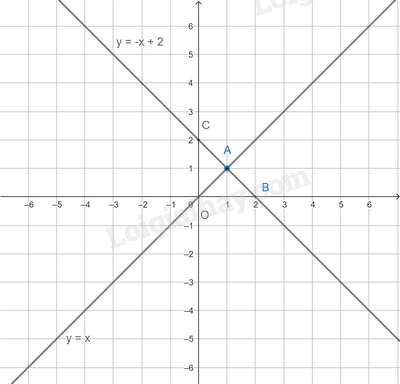
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng y=x và y=−x+2
a) Vẽ hai đường thẳng đã cho trên cùng một mặt phẳng tọa độ
b) Tìm giao điểm A của hai đường thẳng đã cho
c) Gọi B là giao điểm của đường thẳng y=−x+2 và trục Ox. Chứng minh tam giác OAB vuông tại A, tức hai đường thẳng y=x và y=−x+2 vuông góc với nhau
d) Có nhận xét gì về tích hai hệ số góc của hai đường thẳng đã cho

a) Vẽ hai đường thẳng y = x và y = −x + 2 trên mặt phẳng tọa độ bằng cách xác định hai điểm thuộc mỗi đường thẳng.
b) Quan sát đồ thị hàm số y = x và y = 0x + 2 xác định tọa độ điểm A là giao điểm của hai đường thẳng đã cho.
c) Lấy C là giao điểm của đường thẳng y = -x + 2 và trục Oy, chứng minh tam giác OBC vuông cân tại O.
Chứng minh AB = AC => \(OA \bot AB\) hay tam giác OAB vuông cân tại A.
d) Xác định hệ số góc của hai đường thẳng đã cho và tính tích của chúng

a)
* Xét đường thẳng y = x
Cho x = 1 suy ra y = 1 nên điểm (1; 1) thuộc đường thẳng y = x
Đường thẳng y = x đi qua 2 điểm O(0; 0) và (1; 1)\
Advertisements (Quảng cáo)
* Xét đường thẳng y = -x + 2
Cho x = 2 thì y = -2 + 2 = 0 nên điểm (2; 0) thuộc đường thẳng y = - x+ 2
Cho y = 2 suy ra x = 0 nên điểm (0; 2 ) thuộc đường thẳng y = -x + 2
Đường thẳng y = - x + 2 đi qua hai điểm (2; 0) và (0; 2)
b) Gọi A(x0; y0) là giao điểm của hai đường thẳng đã cho. Khi đó, cả hai đường thẳng đã cho đồng thời đi qua điểm A, do đó, ta có:
y0 = x0 và y0 = -x0 + 2, suy ra x0 = −x0 + 2, hay x0 = 1.
Vậy hai đường thẳng đã cho cắt nhau tại điểm A(1;1).
c) Giao điểm của đường thẳng y = -x + 2 và trục Ox là B(2; 0). Suy ra OB = 2.
Vì OA là đường chéo của hình vuông có cạnh bằng 1 nên suy ra OA = \(\sqrt 2 \).
Vì AB là đường chéo của hình vuông có cạnh bằng 1 nên suy ra AB = \(\sqrt 2 \).
Ta có: \(O{A^2} + A{B^2} = {\left( {\sqrt 2 } \right)^2} + {\left( {\sqrt 2 } \right)^2} = 4;O{B^2} = 4.\)
Do đó OA2 + AB2 = OB2, suy ra tam giác OAB vuông tại A (theo định lí Pythagore đảo).
d)
Đường thẳng y = x có hệ số góc bằng 1.
Đường thẳng y = - x + 1 có hệ số góc bằng -1
Tích của hai hệ số góc bằng -1
