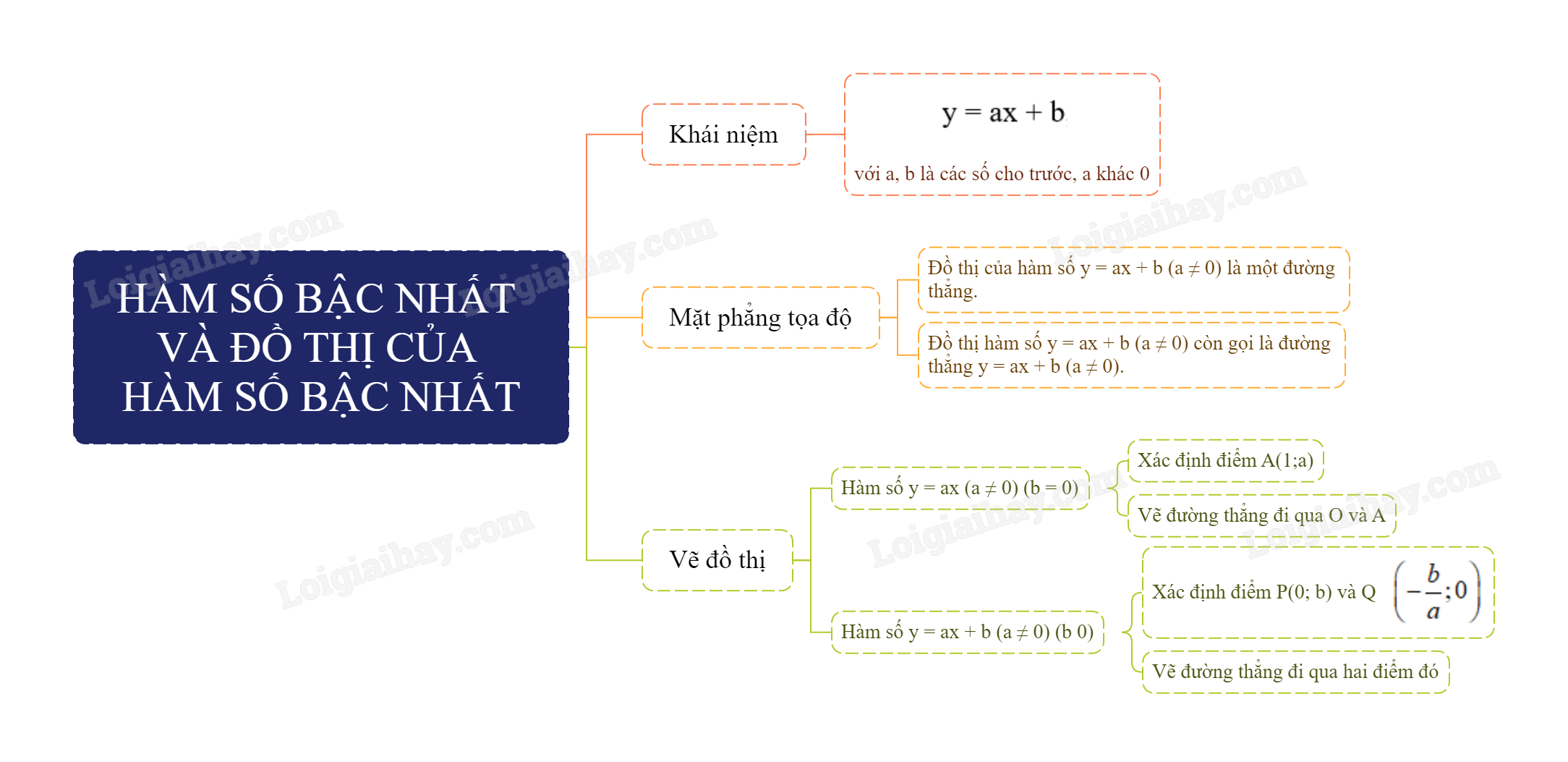
1. Hàm số bậc nhất
Khái niệm:
Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b, trong đó a, b là các số cho trước và a khác 0.
Ví dụ: y = 2x – 3 là hàm số bậc nhất với a = 2 và b = -3
y = x + 4 là hàm số bậc nhất với a = 1, b = 4
2. Mặt phẳng tọa độ
Đồ thị của hàm số y = ax + b (a\( \ne \)0) là một đường thẳng.
Chú ý: Đồ thị hàm số y = ax + b (a\( \ne \)0) còn gọi là đường thẳng y = ax + b (a\( \ne \)0).
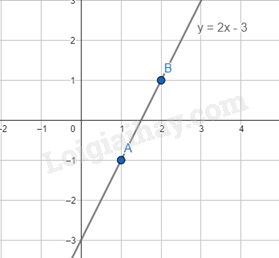
Ví dụ: Cho hàm số y = 2x – 3 có hai điểm A(1, -1) và B(2; 1) thuộc đồ thị của hàm số y = 2x – 3.
3. Vẽ đồ thị của hàm số bậc nhất
Advertisements (Quảng cáo)
Hàm số y = ax (a\( \ne \)0) (b = 0)
Để vẽ đồ thị của hàm số y = ax (a\( \ne \)0), ta có thể xác định điểm A(1; a) rồi vẽ đường thẳng đi qua hai điểm O và A.
Hàm số y = ax + b (a\( \ne \)0) (b\( \ne \)0)
Để vẽ đồ thị của hàm số y = ax + b (a\( \ne \)0, b\( \ne \)0), ta có thể xác định hai điểm P(0; b) và Q\(\left( { - \frac{b}{a};0} \right)\) rồi vẽ dường thẳng đi qua hai điểm đó.
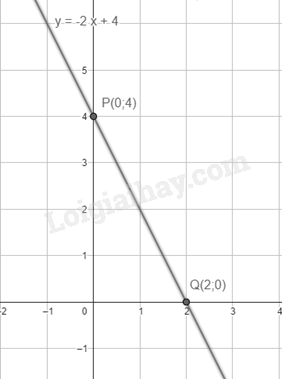
Ví dụ: Cho hàm số y = -2x + 4
Với x = 0 thì y = 4, ta được điểm P(0;4)
Với y = 0 thì x = 22, ta được điểm Q(2;0)
Vậy đồ thị hàm số y = -2x + 4 là đường thẳng đi qua hai điểm P(0;4) và Q(2;0)