Bài 1 trang 45 SBT toán 9 - Chân trời sáng tạo tập 2: Một nhà máy tổ chức thi tuyển kỹ thuật viên mới...

Một nhà máy tổ chức thi tuyển kỹ thuật viên mới. Thời gian hoàn thành một bài thực hành của các ứng viên được ghi lại ở bảng sau (đơn vị: giây).

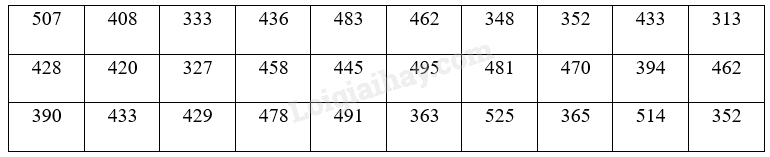
a) Hãy chia số liệu trên thành 5 nhóm với nhóm đầu tiên là [300; 350). Tìm tần số và tần số tương đối của mỗi nhóm

b) Lập bảng tần số ghép nhóm và bảng tần số tương đối ghép nhóm cho mẫu số liệu ghép nhóm đó.

c) Người ta sẽ loại 40% ứng viên có thời gian hoàn thành bài thi lâu nhất. Hỏi các thí sinh có thời gian hoàn thành bài thi trên bao nhiêu giây sẽ bị loại?

Dựa vào: Độ rộng của nhóm là 50 để chia thành 5 nhóm. Đếm số lượng các giá trị của mẫu số liệu để tìm tần số. Công thức tần số tương đối của mỗi nhóm là \(f = \frac{m}{N}.100\% \) (m là tần số nhóm, N là cỡ mẫu).

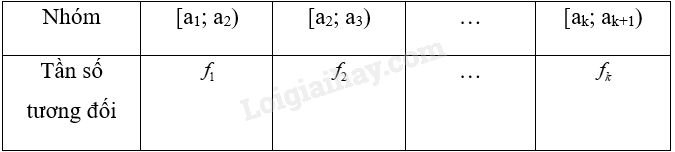
Bảng tần số ghép nhóm có dạng:

Bảng tần số tương đối ghép nhóm có dạng:

Nhìn vào bảng tần số tương đối ghép nhóm để nhận xét.

a) Cỡ mẫu N = 30.

Các nhóm số liệu lần lượt là [300; 350); [350; 400); [400; 450); [450; 500); [500; 550).

Tần số tương đối của 5 nhóm trên lần lượt là m₁ = 4; m₂ = 6; m₃ = 8; m₄ = 9; m₅ = 3.

Gọi \({f_1},{f_2},{f_3},{f_4},{f_5}\) lần lượt là tần số tương đối của các nhóm số liệu trên.

Ta có:

\(\begin{array}{l}{f_1} = \frac{4}{{30}}.100\% = 13,3\% ;{f_2} = \frac{6}{{30}}.100\% = 20\% ;{f_3} = \frac{8}{{30}}.100\% = 26,7\% \\{f_4} = \frac{9}{{30}}.100\% = 30\% ;{f_5} = \frac{3}{{30}}.100\% = 10\% \end{array}\)

b) Bảng tần số ghép nhóm

c) Tần số tương đối của các ứng viên có thời gian hoàn thành bài thi từ 450 giây trở lên là 30% + 10% = 40%.

Vậy các ứng viên có thời gian hoàn thành bài thi từ 450 giây trở lên sẽ bị loại.