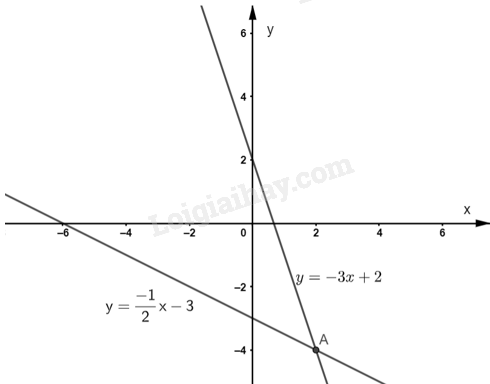
Cho hai đường thẳng \(y = - \frac{1}{2}x - 3\) và y = -3x + 2. Vẽ hai đường thẳng đó trên cùng một hệ trục toạ độ. Xác định toạ độ giao điểm A của hai đường thẳng và cho biết toạ độ của điểm A có là nghệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + 2y = - 6}\\{3x + y = 2}\end{array}} \right.\) không. Tại sao?

Xét phương trình hoành độ giao điểm để tìm giao điểm A và thay vào hệ phương trình để kiểm tra.
Vẽ hai đường thẳng trên trục toạ độ.
Advertisements (Quảng cáo)

Toạ độ giao điểm A của hai đường thẳng là A(2;-4).
Viết lại \(y = - \frac{1}{2}x - 3\) thành x + 2y = -6 và y = - 3x + 2 thành 3x + y = 2.
Vậy toạ độ giao điểm A(2; - 4) là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + 2y = - 6}\\{3x + y = 2}\end{array}} \right.\).