
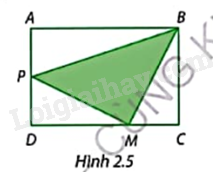
\(ABCD\) là hình chữ nhật có chiều dài \(AB = 6cm\) và chiều rộng \(AD = 4cm\). \(P\) là trung điểm cạnh \(AD\). Tìm điểm \(M\) trên cạnh \(CD\) sao cho diện tích tam giác \(BMP\) không lớn hơn một phần ba diện tích hình chữ nhật \(ABCD\) (Hình 2.5).

Dựa vào các giải bất phương trình để giải bài toán.

Gọi độ dài cạnh \(DM\) là \(x\left( {cm} \right)\).
Diện tích hình chữ nhật \(ABCD\) là: \(AB.AD = 6.4 = 24\left( {c{m^2}} \right)\).
Advertisements (Quảng cáo)
Diện tích tam giác \(APB\) là: \(\frac{1}{2}AP.AB = \frac{1}{2}.2.6 = 6\left( {c{m^2}} \right)\).
Diện tích tam giác \(PDM\) là: \(\frac{1}{2}PD.DM = \frac{1}{2}.2.x = x\left( {c{m^2}} \right)\).
Diện tích tam giác \(BMC\) là: \(\frac{1}{2}.4.\left( {6 - x} \right) = 2\left( {6 - x} \right) = 12 - 2x\left( {c{m^2}} \right)\).
Diện tích tam giác \(PBM\) là: \(24 - 6 - x - \left( {12 - 2x} \right) = 18 - x - 12 + 2x = x + 6\left( {c{m^2}} \right)\).
Để diện tích tam giác \(BMP\) không lớn hơn một phần ba diện tích hình chữ nhật \(ABCD\) thì:
\(\begin{array}{l}x + 6 \le \frac{1}{3}.24\\x + 6 \le 8\\x \le 2\end{array}\)
Vậy điểm \(M\) nằm cách điểm \(D\) nhiều nhất là \(2cm\) thì diện tích tam giác \(BMP\) không lớn hơn một phần ba diện tích hình chữ nhật \(ABCD\).
