Hoạt động (HĐ) 4
Hướng dẫn giải câu hỏi Hoạt động 4 trang 74 SGK Toán 9 Cùng khám phá
Bước 1: Cắt miếng bìa như Hình 9.27a rồi uốn miếng bìa lại và dán hai mép OA, OB sao cho chúng chồng khít lên nhau tạo thành mặt xung quanh của hình nón đỉnh O (không có đáy) như Hình 9.27b.
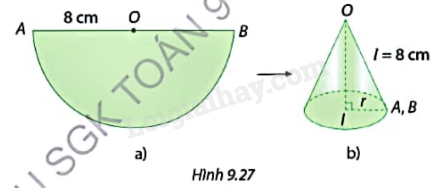
Bước 2: Tính bán kính đáy r của hình nón tạo thành và cắt miếng bìa hình tròn bán kính r. Dùng băng dính dán miếng bìa này với mặt xung quanh của hình nón ở Bước 1 để tạo lập thành một hình nón.

Đọc kĩ dữ kiện đề bài và làm theo.

Luyện tập (LT) 4
Giải câu hỏi Luyện tập 4 trang 75 SGK Toán 9 Cùng khám phá
Tạo lập hình nón có bán kính đáy 5 cm và đường sinh 12 cm. Tính thể tích của hình nón vừa tạo lập.

Tính diện tích xung quanh hình nón, sau đó tính cung n và tạo lập theo các bước sau:
Cắt một miếng bìa hình quạt bán kính r giới hạn bởi cung 90o (một phần tư hình tròn bán kính r) và uốn miếng bìa tạo thành mặt xung quanh của hình nón.
Advertisements (Quảng cáo)
Cắt một miếng bìa hình tròn bán kính r’ cm và dùng băng dính dán miếng bìa này với mặt xung quanh của hình nón vừa tạo.
Thể tích hình nón: \(V = \frac{1}{3}\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình nón).

Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi rn = \pi .5.12 = 60\pi \) cm2
Mặt xung quanh của hình nón trên là hình quạt tròn bán kính 12 cm giới hạn bởi cung no.
Ta có: \(\frac{{\pi {{.12}^2}.n}}{{360}} = 60\pi \) hay \(\frac{{2n}}{5} = 60\). Suy ra n = 150.
Từ đó, tạo lập hình nón trên theo các bước sau:
Cắt một miếng bìa hình quạt bán kính 12 cm giới hạn bởi cung 90o (một phần tư hình tròn bán kính 12 cm) và uốn miếng bìa tạo thành mặt xung quanh của hình nón.
Cắt một miếng bìa hình tròn bán kính 5 cm và dùng băng dính dán miếng bìa này với mặt xung quanh của hình nón vừa tạo.
Chiều cao của hình nón là:
\(\sqrt {{{12}^2} - {5^2}} = \sqrt {119} \) cm
Thể tích hình nón là:
\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.5^2}\sqrt {119} \approx 285,6\) cm3.
