Bài 17.10 trang 31, 32, 33 SBT Vật lý 10 - Kết nối tri thức: Một chú khỉ diễn xiếc treo mình cân bằng trên dây thừng như Hình 17.3...

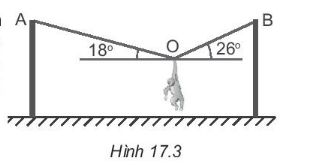
Một chú khỉ diễn xiếc treo mình cân bằng trên dây thừng như Hình 17.3. Xác định lực căng xuất hiện trên các đoạn dây OA, OB. Biết chú khỉ có khối lượng 7 kg. Lấy g = 9,8 m/s².

Viết phương trình cân bằng lực: \(\overrightarrow {{T_1}} + \overrightarrow {{T_2}} + \overrightarrow P = \overrightarrow 0 \).

Tổng hợp các lực theo quy tắc hình bình hành.

Chọn hệ trục Oxy có chiều dương hướng lên (Oy) và hướng từ trái sang phải (Ox).

Chiếu phương trình lần lượt lên chiều (+) của trục Oy, Ox. Giải hệ phương trình.

Sử dụng công thức: P = mg để tính P.

Theo công thức tính trọng lượng, ta có: P = mg = 68,6 N.

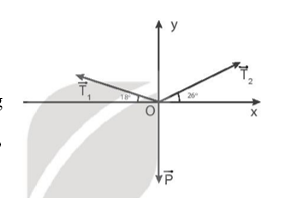
Khi vật cân bằng, ta có phương trình cân bằng lực sau: \(\overrightarrow {{T_1}} + \overrightarrow {{T_2}} + \overrightarrow P = \overrightarrow 0 \).

Chọn hệ trục Oxy có chiều dương hướng lên (Oy) và hướng từ trái sang phải (Ox).

Các lực thành phần theo trục Oy cân bằng nhau:

T₁sin18^o + T₂sin26^o – P = 0 (1)

Các lực thành phần theo trục Ox cân bằng nhau:

T₁cos18^o = T₂cos26^o (2)

Từ (1) và (2) => T₁ = 88,6 N; T₂ = 93,9 N.

Vậy lực căng xuất hiện trên đoạn dây OA có độ lớn T₁ = 88,6 N; lực căng xuất hiện trên đoạn dây OB có độ lớn bằng T₂ = 93,9 N.