Câu hỏi/bài tập:
Hình 7.5 vẽ đồ thị chuyển động của ba vật.
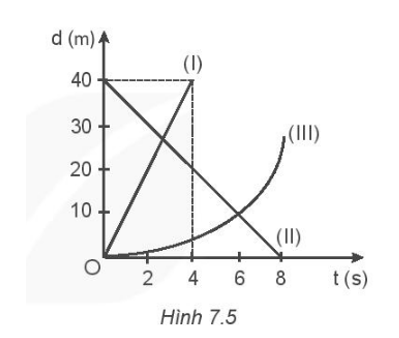
a) Vật nào chuyển động thẳng đều, vật nào chuyển động không đều?
b) Tính vận tốc của vật (1) và (II).
c) Lập phương trình chuyển động của
vật (1) và (II).
d) Xác định vị trí và thời điểm vật (1) gặp vật (II).

Dựa vào đồ thị để xác định vật chuyển động thẳng đều.
Sử dụng công thức tính vận tốc: v = \(\frac{{\Delta d}}{{\Delta t}}\).
Viết phương trình chuyển động của vật theo công thức: d = d0 + vt
Advertisements (Quảng cáo)
Cho phương trình chuyển động của 2 vật bằng nhau. Giải phương trình. Từ đó tìm ra vị trí và thời điểm gặp nhau của 2 vật.

a) (I) và (II) chuyển động thẳng đều vì có đồ thị dịch chuyển – thời gian là đường thẳng.
(III) là chuyển động thẳng không đều vì đồ thị độ dịch chuyển thời gian là đường cong.
b) vI = \(\frac{{\Delta d}}{{\Delta t}}\)=\(\frac{{{d_2} - {d_1}}}{{{t_2} - {t_1}}}\)=\(\frac{{40 - 0}}{{4 - 0}}\)=\(\frac{{40}}{4}\)=10 m/s.
vII = \(\frac{{\Delta d}}{{\Delta t}}\)=\(\frac{{{d_2} - {d_1}}}{{{t_2} - {t_1}}}\)=\(\frac{{0 - 40}}{{8 - 0}}\)=\(\frac{{ - 40}}{8}\)= -5 m/s.
c) Phương trình chuyển động được xác định theo công thức: d = d0 + vt
dI = d0I + vIt = 10t (m)
dII = d0II + vIIt = 40 – 5t (m)
d) (I) và (II) gặp nhau tại điểm M khi: dI = dII \( \Leftrightarrow \) 10t = 40 – 5t
\( \Leftrightarrow \) t ≈ 2,67 s => dI ≈ 26,7 m
Vậy vật (I) và (II) gặp nhau sau 2,67 s tại vị trí cách điểm khởi hành của vật (I) 26,7 m.
