Hoạt động 4
Quan sát hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ở hình 42.
a) Nhận xét về phương của hai vectơ đó.
b) Nhận xét về hướng của hai vectơ đó.
c) So sánh độ dài của hai vectơ đó.
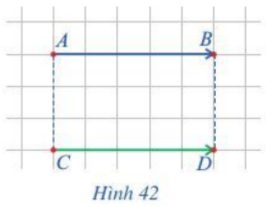

a) Nhận xét về giá của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), chỉ ra chúng cùng phương.
b) Nhận xét về hướng của hai vectơ đó (hướng sang phải/trái)
c) Độ dài của vectơ \(\overrightarrow {AB} \) là độ dài đoạn thẳng AB.

a) Ta có:
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Advertisements (Quảng cáo)
Dễ thấy: AB // CD do đó hai vectơ này cùng phương.
b) Quan sát hình 42, ta thấy cả hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng sang phải
Như vậy hai vectơ này cùng hướng.
c) Ta có: \(|\overrightarrow {AB} |\; = AB\); \(|\overrightarrow {CD} |\; = CD\) và AB = CD (cùng dài 5 ô vuông)
Vậy độ dài của hai vectơ là bằng nhau.
Luyện tập – vận dụng 2
Cho tam giác ABC. Vẽ điểm D thỏa mãn \(\overrightarrow {AD} = \overrightarrow {BC} .\) Tứ giác ABCD là hình gì?

Hai vectơ \(\overrightarrow {AD} ,\;\overrightarrow {BC} \)bằng nhau nếu chúng cùng hướng và cùng độ dài.

Ta có: \(\overrightarrow {AD} = \overrightarrow {BC} .\)
\( \Rightarrow \left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\)
Do đó tứ giác ABCD có một cặp cạnh đối song và bằng nhau
Vậy tứ giác ABCD là hình bình hành.
