
Cho hình chóp S. ABC. Gọi D, E, F lần lượt là ba điểm trên ba cạnh SA, SB, SC sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K. Chứng minh ba điểm I, J, K thẳng hàng.

Sử dụng kiến thức về tính chất được thừa nhận trong không gian để chứng minh ba điểm thẳng hàng: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.

Advertisements (Quảng cáo)
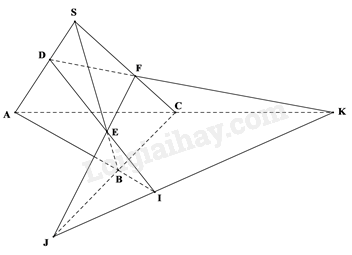
Vì \(I \in AB \Rightarrow I \in \left( {ABC} \right),I \in DE \Rightarrow I \in \left( {DEF} \right)\)
Vì \(J \in BC \Rightarrow I \in \left( {ABC} \right),J \in EF \Rightarrow J \in \left( {DEF} \right)\)
Vì \(K \in AC \Rightarrow I \in \left( {ABC} \right),K \in DF \Rightarrow I \in \left( {DEF} \right)\)
Vì 3 điểm I, J, K cùng thuộc hai mặt phẳng (ABC) và (DEF) nên ba điểm I, J, K thẳng hàng.
