
Cho hình chóp S. ABCD có ABCD là hình thang đáy lớn AD. Gọi E, F lần lượt là hai điểm trên hai cạnh SB, SD.
a) Tìm giao điểm EF với (SAC).
b) Tìm giao điểm BC với (AEF).

Sử dụng kiến thức về giao điểm giữa đường thẳng và mặt phẳng để tìm: Cách tìm giao điểm của đường thẳng d và mặt phẳng \(\left( \alpha \right)\):
- Trường hợp 1: Trong mặt phẳng \(\left( \alpha \right)\) có sẵn đường thẳng d’ cắt d tại I: Ta có ngay \(d \cap \left( \alpha \right) = I\)
- Trường hợp 2: Trong mặt phẳng \(\left( \alpha \right)\) không có sẵn đường thẳng d’ cắt d. Khi đó ta thực hiện như sau:
+ Chọn mặt phẳng phụ \(\left( \beta \right)\) chứa d và \(\left( \beta \right)\) cắt \(\left( \alpha \right)\) theo giao tuyến d’.
Advertisements (Quảng cáo)
+ Gọi \(I = d’ \cap d\). Khi đó, \(d \cap \left( \alpha \right) = I\).

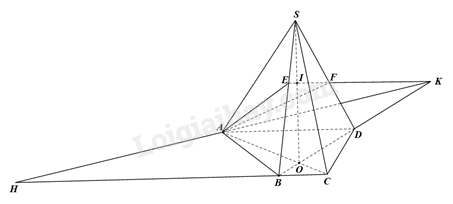
a) Trong mặt phẳng (ABCD), gọi O là giao điểm của AC và BD. Do đó, SO là giao tuyến của mặt phẳng (SAC) và (SBD).
Trong mặt phẳng (SBD), gọi I là giao điểm của EF và SO.
Vì I thuộc EF, \(I \in SO \subset \left( {SAC} \right)\) nên I là giao điểm của EF và (SAC).
b) Trong mặt phẳng (SBD), gọi K là giao điểm của EF và BD. Khi đó, AK là giao tuyến của (ABCD) và (AEF).
Trong mặt phẳng (ABCD), gọi H là giao điểm của BC và AK.
Vì H thuộc BC, \(H \in AK \subset \left( {AEF} \right)\) nên H là giao điểm của BC và (AEF).
