
Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\); I, J lần lượt là trung điểm của BD, CD.
a) Chứng minh rằng MN//BC.
b) Tứ giác MNJI là hình gì. Tìm điều kiện để tứ giác MNJI là hình bình hành.

Sử dụng kiến thức về tính chất cơ bản về hai đường thẳng song song để chứng minh: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.

Advertisements (Quảng cáo)
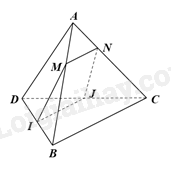
a) Tam giác ABC có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) nên MN//BC (định lý Thalès đảo)
b) Vì I, J lần lượt là trung điểm của BD, CD nên IJ là đường trung bình của tam giác BCD. Do đó, IJ//BC
Mà MN//BC nên IJ//MN, do đó, MNJI là hình thang.
Hình thang MNJI là hình bình hành khi và chỉ khi MI//NJ//AD.
Mà I là trung điểm của BD. Do đó, MI là đường trung bình của tam giác ADB.
Suy ra M là trung điểm của AB.
