
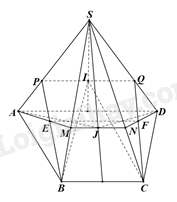
Cho hình chóp S. ABCD có đáy ABCD là hình thang, đáy lớn AD. Gọi I và J lần lượt trọng tâm của tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD tại P, Q.
a) Chứng minh MN song song với PQ.
b) Gọi E là giao điểm của AM và BP, F là giao điểm của CQ và DN. Chứng minh EF song song với MN và PQ.

Sử dụng kiến thức về tính chất cơ bản về hai đường thẳng song song để chứng minh:
+ Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
+ Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.

Advertisements (Quảng cáo)
a) Ta có: AD//BC (do ABCD là hình thang đáy lớn AD).
Mà \(AD \subset \left( {ADJ} \right),BC \subset \left( {SBC} \right),\left( {ADJ} \right) \cap \left( {SBC} \right) = MN\)
Do đó, MN//AD//BC
Chứng minh tương tự ta có: PQ//AD//BC
Suy ra: MN//PQ
b) Ta có: AD//BC (do ABCD là hình thang đáy lớn AD).
Mà \(AD \subset \left( {ADJ} \right),BC \subset \left( {IBC} \right),\left( {ADJ} \right) \cap \left( {IBC} \right) = EF\) nên EF//AD//BC
Mà MN//PQ// AD//BC (theo câu a)
Do đó, MN//EF//QP
