
Thầy giáo thống kê lại số lần kéo xà đơn của các học sinh nam khối 11 ở bảng sau:

a) Hãy ước lượng số trung bình, mốt và trung vị của mẫu số liệu ghép nhóm trên.
b) Thầy giáo dự định chọn 25% học sinh có số lần kéo thấp nhất để bồi dưỡng thể lực thêm. Thầy giáo nên chọn học sinh có thành tích kéo xà đơn dưới bao nhiêu lần để bồi dưỡng thể lực?

Sử dụng kiến thức về số trung bình của mẫu số liệu để tính:
Giả sử mẫu số được cho dưới dạng bảng tần số ghép nhóm:
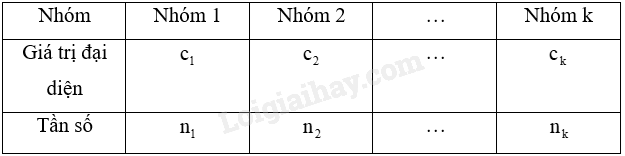
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau: \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}}}{n}\), trong đó \(n = {n_1} + {n_2} + ... + {n_k}\).
+ Sử dụng kiến thức xác định trung vị của mẫu số liệu ghép nhóm để tính:
Gọi n là cỡ mẫu.
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa trung vị, \({n_m}\) là tần số của nhóm chứa trung vị,
\(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khi đó, trung vị của mẫu số liệu là: \({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).
+ Sử dụng kiến thức về xác định tứ phân vị của mẫu số liệu ghép nhóm để tính:
Tứ phân vị thứ hai của mẫu số liệu ghép nhóm, kí hiệu \({Q_2}\), cũng chính là trung vị của mẫu số liệu ghép nhóm.
b) Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu \({Q_1}\), ta làm như sau:
Advertisements (Quảng cáo)
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa tứ phân vị thứ nhất, \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ nhất, \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\)
Khi đó, tứ phân vị thứ nhất của mẫu số liệu là: \({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\)

Ta hiệu chỉnh lại bảng số liệu bao gồm giá trị đại diện:

Cỡ mẫu \(n = 143\)
Số trung bình của mẫu số liệu là: \(\overline x = \frac{{8.35 + 13.54 + 18.32 + 23.17 + 28.5}}{{143}} = \frac{{2\;089}}{{143}}\)
Nhóm chứa mốt của mẫu số liệu là \(\left[ {10,5;15,5} \right)\).
Do đó, \({u_m} = 10,5,{u_{m + 1}} = 15,5,{n_m} = 54,{n_{m - 1}} = 35,{n_{m + 1}} = 32,{u_{m + 1}} - {u_m} = 15,5 - 10,5 = 5\)
Mốt của mẫu số liệu là: \({M_O} = 10,5 + \frac{{54 - 35}}{{\left( {54 - 35} \right) + \left( {54 - 32} \right)}}.5 = \frac{{1051}}{{82}}\).
Gọi \({x_1},{x_2},...,{x_{143}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_{35}} \in \left[ {5,5;10,5} \right),{x_{36}},...,{x_{89}} \in \left[ {10,5;15,5} \right),{x_{90}},...,{x_{121}} \in \left[ {15,5;20,5} \right),\)\({x_{122}},...,{x_{138}} \in \left[ {20,5;25,5} \right),{x_{139}},...,{x_{143}} \in \left[ {25,5;30,5} \right)\)
Do cỡ mẫu \(n = 143\) nên trung vị \({M_e} = {x_{72}} \in \left[ {10,5;15,5} \right)\) nên trung vị của mẫu số liệu là:
\({M_e} = 10,5 + \frac{{\frac{{143}}{2} - 35}}{{54}}.\left( {15,5 - 10,5} \right) = \frac{{1499}}{{108}}\)
b) Do cỡ mẫu \(n = 143\) nên tứ phân vị thứ nhất của mẫu số liệu là \({x_{36}}\). Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm \(\left[ {10,5;15,5} \right)\).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 10,5 + \frac{{\frac{{143}}{4} - \left( {35 + 0} \right)}}{{54}}.\left( {15,5 - 10,5} \right) = \frac{{761}}{{72}} \approx 10,57\)
Vậy giáo viên nên chọn các bạn có thành tích kéo xà dưới 11 lần để bồi dưỡng thể lực thêm.
