Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, cho điểm M thay đổi trên cạnh SD
Câu 1. ( 3 điểm)
Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC)
Câu 2. ( 3 điểm)
Xác định giao điểm N của SC và mặt phẳng (ABM). Tứ giác ABNM là hình gì? Có thể là hình bình hành không?
Câu 3. ( 4 điểm)
Gọi I, J lần lượt là giao điểm của AN với BM và AM với BN. Chứng minh rằng khi M chạy trên cạnh SD thì I, J lần lượt chạy trên các đường thẳng cố định.

Advertisements (Quảng cáo)
Câu 1.
Hai mặt phẳng (SAD) và (SBC) có điểm chung S và lần lượt chứa hai đường thẳng song song ADvà BC nên giao tuyến của chúng là đường thẳng d đi qua S và song song với AD và BC.
Câu 2.
Hai mặt phẳng (MAB) và (SCD) có điểm chung M và lần lượt chứa hai đường thẳng song song AB và CD nên giao tuyến của chúng là đường thẳng d đi qua M và song song vớiAB và CD. Vậy qua M ta vẽ đường thẳng d’, đường thẳng này cắt SC tại N. Đây là điểm cần tìm. Ta thấy ngay ABNM là hình thang. Để ABNM là hình bình hành ta phải có thêm AM song song với BN. Khi đó AM và BN phải song song với d. Điều này không thể xảy ra khi M thuộc đoạn SD và không trùng với hai đầu mút S và D.
Câu 3.
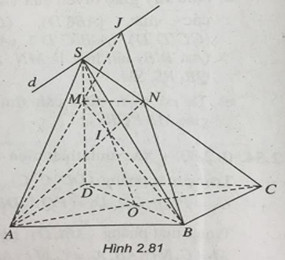
\(I = AN \cap BM\) nên I lần lượt thuộc hai mặt phẳng (SAC) và (SBD).Như vậy I phải thuộc giao tuyến SO của hai mặt phẳng này, ở đây \(O = AC \cap B{\rm{D}}\). Tương tự , ta có J thuộc d (h.2.81).
