Bài I.13 trang 17, 18 Sách bài tập Vật Lý 11: Một điện tích điểm q1 = +9.10-8 C nằm tại điểm A trong chân không....

Một điện tích điểm q₁ = +9.10^-8 C nằm tại điểm A trong chân không. Một điện tích điểm khác q_o = -16.10^-8 C nằm tại điểm B trong chân không. Khoảng cách AB là 5 cm.

a) Xác định cường độ điện trường tại điểm C với CA = 3 cm và CB = 4 cm.

b) Xác định điểm D mà tại đó cường độ điện trường bằng 0.

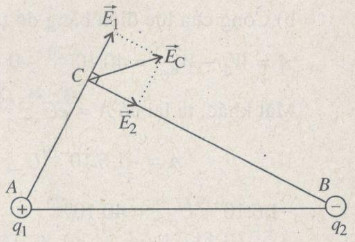
a) Nhận xét thấy AB² = CA² + CB². Do đó, tam giác ABC vuông góc ở C.

Vectơ cường độ điện trường do q₁ gây ra ở C có phương nằm dọc theo AC, chiều hướng ra xa q₁ và cường độ là :

\({E_1} = k{{\left| {{q_1}} \right|} \over {A{C^2}}} = {9.10^9}.{{{{9.10}^{ - 8}}} \over {{{9.10}^{ - 4}}}} = {9.10^5}V/m\)

Vectơ cường độ điện trường do q₂ gây ra ở C có phương nằm dọc theo BC, chiều hướng về q₂ và cường độ :

\({E_2} = k{{\left| {{q_2}} \right|} \over {B{C^2}}} = {9.10^9}.{{{{16.10}^{ - 8}}} \over {{{16.10}^{ - 4}}}} = {9.10^5}V/m\)

Vectơ cường độ điện trường tổng hợp tại C là :

\(\overrightarrow {{E_C}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)

Hình bình hành mà hai cạnh là hai vectơ \(\overrightarrow {{E_1}} \)  và \(\overrightarrow {{E_2}} \)  trở thành một hình vuông mà \(\overrightarrow {{E_C}} \) nằm dọc theo đường chéo qua C.

Vậy :

\(\eqalign{
& {E_C} = {E_1}\sqrt 2 = 9\sqrt 2 {.10^5}V/m \cr
& {E_C} \approx {12,7.10^5}V/m \cr} \)

E_c ≈ 12,7.10⁵ V/m Phương và chiều của vectơ \(\overrightarrow {{E_C}} \) được vẽ trên Hình I.2G.

b) Tại D ta có \(\overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = \overrightarrow 0 \)

 hay  \(\overrightarrow {{E_1}} = - \overrightarrow {{E_2}} \)

Hai vectơ  \(\overrightarrow {{E_1}} \)  và \(\overrightarrow {{E_2}} \) có cùng phương, ngược chiều và cùng cường độ. Vậy điểm D phải nằm trên đường thẳng AB và ngoài đoạn AB. Vì |q₂| > |q₁| nên D phải nằm xa hơn (Hình I.3G).

Đặt DA = x và AB = a = 5 cm ; ta có:

\({E_1} = {{k\left| {{q_1}} \right|} \over {{x^2}}};{E_2} = {{k\left| {{q_2}} \right|} \over {{{(a + x)}^2}}};\)

Với E₁ = E₂ thì (a + x)²|q₁| = x²|q₂|

\(\eqalign{
& (a + x)\sqrt {\left| {{q_1}} \right|} = x\sqrt {\left| {{q_2}} \right|} \cr
& (a + x)\sqrt {{{9.10}^{ - 8}}} = x\sqrt {{{16.10}^{ - 8}}} \cr
& 3(a + x) = 4x \cr
& x = 3a = 15cm \cr} \)

Ngoài ra còn phải kể đến tất cả các điểm nằm rất xa hai điện tích q₁ và q₂.