
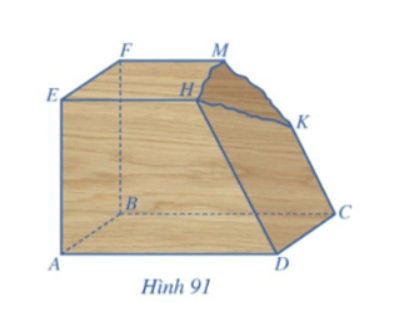
Một khối gỗ có các mặt đều là một phần của mặt phẳng với (ABCD) // (EFGH), CK // DH. Khối gỗ bị hỏng một góc (Hình 91). Bác thợ mộc muốn làm đẹp khối gỗ bằng cách cắt khối gỗ theo mặt phẳng (R) đi qua K và song song với mặt phẳng (ABCD).
a) Hãy giúp bác thợ mộc xác định giao tuyến của mặt phẳng (R) với các mặt của khối gỗ để cắt được chính xác.
b) Gọi I, J lần lượt là giao điểm DH, BF với mặt phẳng (R). Biết BF = 60 cm, DH = 75 cm, CK = 40 cm. Tính FJ.

a, Tìm 2 điểm thuộc 2 mặt phẳng (P), (Q). Đường thẳng nối 2 điểm đó được gọi là giao tuyến của (P) và (Q).
b, Quan sát hình vẽ.

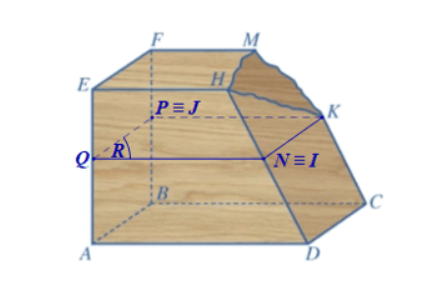
a) Trong mp(CDHK), qua K vẽ đường thẳng song song với CD, cắt DH tại N.
Trong mp(BCKF), qua K vẽ đường thẳng song song với BC, cắt BF tại P.
Ta có: NK // CD, mà CD ⊂ (ACBD) nên NK // (ABCD).
KP // BC, mà BC ⊂ (ACBD) nên KP // (ABCD).
NK, KP cắt nhau tại K trong mp(NPK).
Do đó (NPK) // (ABCD).
Khi đó mp(R) qua K và song song với (ABCD) chính là mp(NPK).
Advertisements (Quảng cáo)
Trong mp(ADHE), qua N vẽ đường thẳng song song với AD, cắt AE tại Q.
Khi đó mp(R) là mp(NKPQ).
Vậy: (NKPQ) ∩ (ADHE) = QN;
(NKPQ) ∩ (CDHK) = NK;
(NKPQ) ∩ (BCKF) = KP;
(NKPQ) ∩ (ABFE) = PQ.
b)Ta có: DH cắt NK tại N, mà NK ⊂ (R) nên giao điểm của DH và (R) là điểm N.
Theo bài, I là giao điểm của DH và (R) nên điểm I và điểm N trùng nhau.
Tương tự ta cũng có điểm J trùng với điểm P.
Ta có: (ABCD) // (EFMH) và (R) // (ABCD) nên (EFMH) // (R) // (ABCD).
Lại có, hai cát tuyến FB, HD cắt ba mặt phẳng song song (EFMH), (R), (ABCD) lần lượt tại F, J, B và H, I, D nên theo định lí Thalès ta có: \(\frac{{FJ}}{{HI}} = \frac{{FB}}{{HD}}\) .
Mặt khác, trong mp(CDKH), tứ giác CDIK có CK // DI (do CK // DH) và IK // CD
Do đó CDIK là hình bình hành, suy ra DI = CK = 40 cm.
Khi đó HI = DH – DI = 75 – 40 = 35 (cm).
Vì vậy, từ \(\frac{{FJ}}{{HI}} = \frac{{FB}}{{HD}}\) ta có: \(\frac{{FJ}}{{35}} = \frac{{60}}{{75}}\) , suy ra \(FJ = \frac{{35.60}}{{75}} = 28\) (cm).
Vậy FJ = 28 cm.
