Dựa vào các xác định góc giữa hai đường thẳng đã học để làm . Trả lời bài 3 trang 79 SGK Toán 11 tập 2 - Cánh Diều Bài 1. Hai đường thẳng vuông góc. Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và (widehat {SAB} = 100^circ ) (Hình 8)...

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và \(\widehat {SAB} = 100^\circ \) (Hình 8) . Tính góc giữa hai đường thẳng:
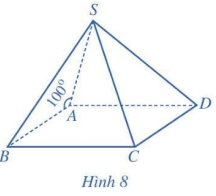
a) SA và AB
b) SA và CD

Dựa vào các xác định góc giữa hai đường thẳng đã học để làm

Advertisements (Quảng cáo)
Cách giải:
a) Vì \( \widehat {SAB} = 100^\circ \) nên
\(\left( {SA,AB} \right) = 180^0 - \widehat {SAB} = 180^0 - 100^\circ = 80^0 \)
Vậy góc giữa hai đường thẳng SA và AB bằng \( 80^0 \)
b) Do ABCD là hình bình hành => AB // CD
\( \Rightarrow \left( {SA, CD} \right) = \left( {SA, AB} \right) = 80^\circ \)
Vậy góc giữa hai đường thẳng SA và CD bằng \( 80^0 \)
