Dựa vào định lí vừa học để chứng minh . Trả lời bài 5 trang 88 SGK Toán 11 tập 2 – Cánh Diều Bài 2. Đường thẳng vuông góc với mặt phẳng. Cho hình chóp O. ABC có (widehat {AOB} = widehat {BOC} = widehat {COA} = 90^circ ). Chứng minh rằng...
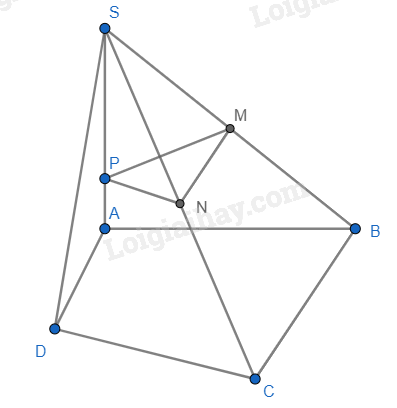
Cho hình chóp S.ABCD có SA \(\bot\) (ABC), BC \(\bot\) AB. Lấy hai điểm M, N lần lượt là trung điểm của SB, SC và điểm P nằm trên cạnh SA. Chứng minh rằng tam giác MNP là tam giác vuông.
Dựa vào định lí vừa học để chứng minh
Vì SA \(\bot\) (ABCD) nên AB là hình chiếu của SB trên mặt phẳng (ABCD). Mà BC \(\bot\) AB nên theo định lí ba đường vuông góc ta có SB \(\bot\) BC.
Mà BC // MN (do MN là đường trung bình của tam giác SBC)
=> SB \(\bot\) MN. (1)
Ta có SA \(\bot\) (ABC) => SA \(\bot\) BC, mà BC // MN => SA \(\bot\) MN. (2)
Từ (1) và (2) suy ra MN \(\bot\) (SAB) => MN \(\bot\) MP hay tam giác MNP là tam giác vuông tại M.