Hoạt động2
Quan sát hình ảnh một quyển sổ được mở ra (Hình 35), mỗi trang sổ gợi nên hình ảnh của một nửa mặt phẳng. Nêu đặc điểm của hai nửa mặt phẳng đó.


Dựa vào khái niệm góc nhị diện.

Hai nửa mặt phẳng đó có chung bờ là đường thẳng chứa gáy sổ.
Hoạt động3
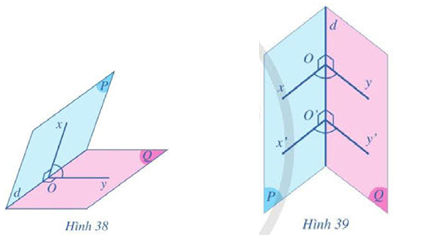
Cho góc nhị diện có hai mặt là hai nửa mặt phẳng \(\left( P \right),\left( Q \right)\) và cạnh của góc nhị diện là đường thẳng \(d\).
Qua một điểm \(O\) trên đường thẳng \(d\), ta kẻ hai tia \(Ox,Oy\) lần lượt thuộc hai nửa mặt phẳng \(\left( P \right),\left( Q \right)\) và cùng vuông góc với đường thẳng \(d\). Góc \(xOy\) gọi là góc phẳng nhị diện của góc nhị diện đã cho (Hình 38).
Giả sử góc \(x’Oy’\) cũng là góc phẳng nhị diện của góc nhị diện đã cho với \(O’\) khác \(O\) (Hình 39).
Hãy so sánh số đo của hai góc \(xOy\) và \(x’Oy’\).

Sử dụng quan hệ giữa hai đường thẳng song song.

Trong \(\left( P \right)\) ta có:
\(\left. \begin{array}{l}Ox \bot d\\O’x’ \bot d\end{array} \right\} \Rightarrow Ox\parallel O’x’\)
Trong \(\left( Q \right)\) ta có:
\(\left. \begin{array}{l}Oy \bot d\\O’y’ \bot d\end{array} \right\} \Rightarrow Oy\parallel O’y’\)
Vậy \(\left( {Ox,Oy} \right) = \left( {O’x’,O’y’} \right)\) hay số đo của hai góc \(xOy\) và \(x’Oy’\) bằng nhau.
Luyện tập3
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông và \(SA \bot \left( {ABCD} \right)\). Tính số đo theo đơn vị độ của góc nhị diện:
a) \(\left[ {B,SA,D} \right]\);
Advertisements (Quảng cáo)
b) \(\left[ {B,SA,C} \right]\).

‒ Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).

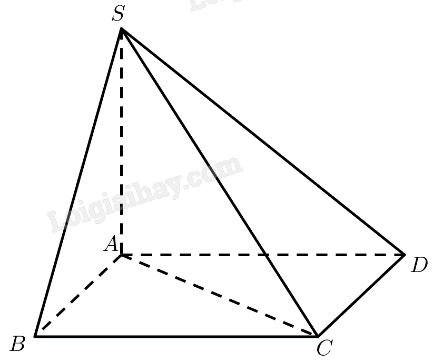
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{D}}\)
Vậy \(\widehat {BA{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,D} \right]\)
\(ABCD\) là hình vuông \( \Rightarrow \widehat {BA{\rm{D}}} = {90^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,D} \right]\) bằng \({90^ \circ }\).
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{C}}\)
Vậy \(\widehat {BA{\rm{C}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,C} \right]\)
\(ABCD\) là hình vuông \( \Rightarrow \widehat {BA{\rm{C}}} = {45^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,C} \right]\) bằng \({45^ \circ }\).
Luyện tập2
Trong không gian cho hai mặt phẳng \((\alpha), (\beta)\) cắt nhau theo giao tuyến d. Hai mặt phẳng \((\alpha), (\beta)\) tạo nên bao nhiêu góc nhị diện có cạnh của góc nhị diện là đường thẳng d?

Dựa vào kiến thức về góc nhị diện.

Số góc nhị diện mà hai mặt phẳng (a) và (B) tạo ra bằng số điểm trên đường thẳng d.
