Hoạt động 3
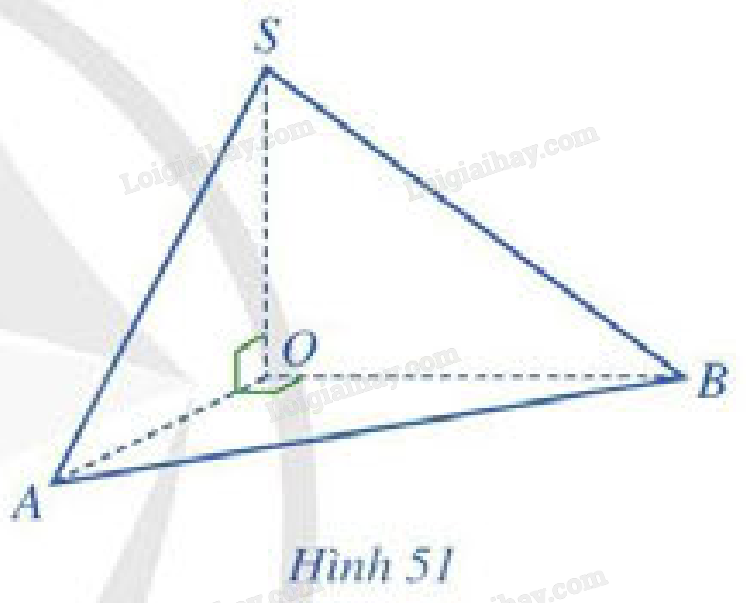
Cho hình chóp \(S.OAB\) thoả mãn \(\left( {AOS} \right) \bot \left( {AOB} \right)\), \(\widehat {AOS} = \widehat {AOB} = {90^ \circ }\) (Hình 51).
a) Giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\) là đường thẳng nào?
b) \(SO\) có vuông góc với giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\) hay không?
c) \(SO\) có vuông góc với mặt phẳng \(\left( {AOB} \right)\) hay không?

‒ Để tìm giao tuyến của hai mặt phẳng, ta có 2 cách:
+ Cách 1: Tìm 2 điểm chung phân biệt. Giao tuyến là đường thẳng đi qua hai điểm chung.
+ Cách 2: Tìm 1 điểm chung và 2 đường thẳng song song nằm trên mỗi mặt phẳng. Giao tuyến là đường thẳng đi qua điểm chung và song song với hai đường thẳng đó.
‒ Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.

a) Ta có:
\(\left. \begin{array}{l}A \in \left( {AOS} \right) \cap \left( {AOB} \right)\\O \in \left( {AOS} \right) \cap \left( {AOB} \right)\end{array} \right\} \Rightarrow AO = \left( {AOS} \right) \cap \left( {AOB} \right)\)
b) \(\widehat {AOS} = {90^ \circ } \Rightarrow SO \bot AO\)
Vậy \(SO\) có vuông góc với giao tuyến của hai mặt phẳng \(\left( {AOS} \right)\) và \(\left( {AOB} \right)\).
c) \(\widehat {AOS} = {90^ \circ } \Rightarrow SO \bot AO\)
\(\widehat {AOB} = {90^ \circ } \Rightarrow AO \bot BO\)
Vậy \(\widehat {SOB}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {S,AO,B} \right]\)
Vì \(\left( {AOS} \right) \bot \left( {AOB} \right)\) nên \(\widehat {SOB} = {90^ \circ }\)
\(\left. \begin{array}{l} \Rightarrow SO \bot OB\\SO \bot OA\end{array} \right\} \Rightarrow SO \bot \left( {AOB} \right)\)
Luyện tập 3
Cho tứ diện \(ABCD\) có \(\left( {ABD} \right) \bot \left( {BCD} \right)\) và \(CD \bot BD\). Chứng minh rằng tam giác \(ACD\) vuông.

Sử dụng định lí 2: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường nào nằm trong mặt phẳng này và vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.

Advertisements (Quảng cáo)
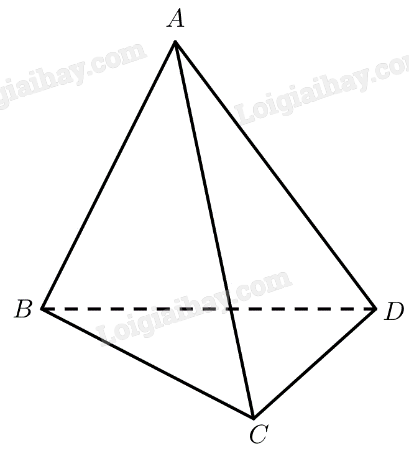
Ta có:
\(\left. \begin{array}{l}\left( {ABD} \right) \bot \left( {BCD} \right)\\\left( {ABD} \right) \cap \left( {BCD} \right) = BD\\C{\rm{D}} \subset \left( {BCD} \right)\\C{\rm{D}} \bot B{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABD} \right) \Rightarrow C{\rm{D}} \bot A{\rm{D}}\)
Vậy tam giác \(ACD\) vuông tại \(D\).
Hoạt động 4
Trong Hình 54, hai bìa của cuốn sách gợi nên hình ảnh hai mặt phẳng vuông góc với mặt bàn. Hãy dự đoán xem gáy sách có vuông góc với mặt bàn hay không.


Quan sát hình ảnh và trả lời câu hỏi.

Gáy sách vuông góc với mặt bàn.
Luyện tập 4
Cho hình chóp \(S.ABC\) có \(SA \bot SB,SB \bot SC,SC \bot SA\). Chứng minh rằng:
a) \(\left( {SAB} \right) \bot \left( {SBC} \right)\);
b) \(\left( {SBC} \right) \bot \left( {SCA} \right)\);
c) \(\left( {SCA} \right) \bot \left( {SAB} \right)\).

Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.

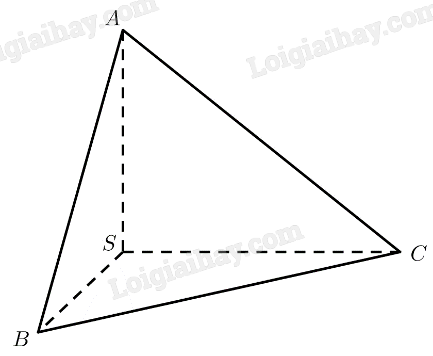
a) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}SA \bot SB\\SA \bot SC\end{array} \right\} \Rightarrow SA \bot \left( {SBC} \right)\\SA \subset \left( {SAB} \right)\end{array} \right\} \Rightarrow \left( {SAB} \right) \bot \left( {SBC} \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}SA \bot SB\\SA \bot SC\end{array} \right\} \Rightarrow SA \bot \left( {SBC} \right)\\SA \subset \left( {SCA} \right)\end{array} \right\} \Rightarrow \left( {SCA} \right) \bot \left( {SBC} \right)\)
c) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}SA \bot SB\\SB \bot SC\end{array} \right\} \Rightarrow SB \bot \left( {SCA} \right)\\SB \subset \left( {SAB} \right)\end{array} \right\} \Rightarrow \left( {SAB} \right) \bot \left( {SCA} \right)\)
