Hoạt động 5
Trong Hình 19, hai thanh sắt và bản phẳng để ngồi gợi nên hình ảnh hai đường thẳng a, b và mặt phẳng (P). Quan sát Hình 19 và cho biết:
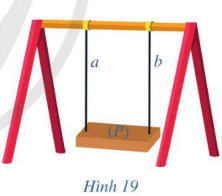
a) Nếu hai đường thẳng a và b song song với nhau và mặt phẳng (P) vuông góc với đường thẳng a thì mặt phẳng (P) có vuông góc với đường thẳng b hay không?
b) Nếu hai đường thẳng a và b cùng vuông góc với mặt phẳng (P) thì chúng có song song với nhau hay không?

Quan sát hình vẽ để trả lời

a, Gọi (Q) là mặt phẳng chứa đường thẳng a, b
Theo tính chất 2 “Có duy nhất 1 đường thẳng đi qua 1 điểm cho trước và vuông góc với một mặt phẳng cho trước”
b, Nếu hai đường thẳng a và b cùng vuông góc với mặt phẳng (P) thì chúng song song với nhau.
Luyện tập - vận dụng 4
Cho đường thẳng d và mặt phẳng (P) cắt nhau tại điểm O. Lấy các điểm A, B thuộc d khác O; các điểm A’, B’ thuộc (P) thỏa mãn \(AA’ \bot (P),\,BB’ \bot (P)\). Chứng minh rằng: \(\frac{{AA’}}{{BB’}} = \frac{{OA}}{{OB}}\)

Sử dụng định lý Thalès: Nếu một đường thẳng song song với một cạnh của tam giác đó và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

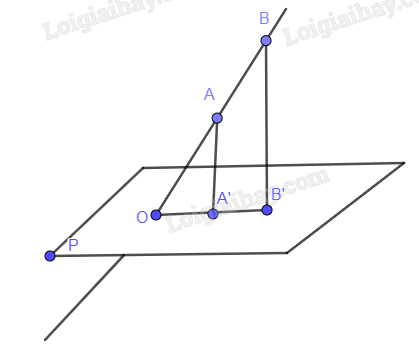
Do \({\rm{AA}}’ \bot (P),\,BB’ \bot (P) \Rightarrow {\rm{AA’ //}}\,{\rm{BB’}}\)
Xét có \({\rm{AA’ //}}\,{\rm{BB’}} \Rightarrow \frac{{{\rm{AA}}’}}{{{\rm{BB’}}}} = \frac{{OA}}{{OB}}\) (Định lý Thalès)
Advertisements (Quảng cáo)
Hoạt động 6
Trong Hình 21 , hai mặt sàn của nhà cao tầng và cột trụ bê tông gợi nên hình ảnh hai mặt phẳng (P), (Q) phân biệt và đường thẳng a.

Quan sát Hình 21 và cho biết:
a) Nếu hai mặt phẳng (P) và (Q) song song với nhau và đường thẳng a vuông góc với mặt phẳng (P) thì đường thẳng a có vuông góc với mặt phẳng (Q) hay không?
b) Nếu hai mặt phẳng (P) và (Q) cùng vuông góc với đường thẳng a thì chúng có song song với nhau hay không?

Quan sát hình vẽ để trả lời

a) Nếu (P) // (Q) và \(a \bot (P)\) thì \(a \bot (Q)\)
b) Nếu hai mặt phẳng (P) và (Q) cùng vuông góc với đường thẳng a thì chúng song song với nhau.
Luyện tập - vận dụng 5
Cho hình chóp S.ABC có SA ⊥ (ABC). Mặt phẳng (P) khác với mặt phẳng (ABC), vuông góc với đường thẳng SA và lần lượt cắt các đường thẳng SB, SC tại hai điểm phân biệt B’, C’. Chứng minh rằng B’C’ // BC

Sử dụng tính chất: \(\left\{ \begin{array}{l}(P) \bot a\\(Q) \bot a\end{array} \right. \Rightarrow (P)\,//\,(Q)\)

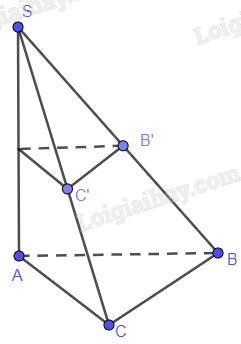
Do \(\left\{ \begin{array}{l}(P) \bot SA\\(ABC) \bot SA\end{array} \right. \Rightarrow (P)\,//\,(ABC) \Rightarrow B’C’\,//BC\)
