Hoạt động 8
Trong Hình 27, mặt sàn gợi nên hình ảnh mặt phẳng (P), đường thẳng a không vuông góc với mặt phẳng (P), đường thẳng a’ là hình chiếu của đường thẳng a trên mặt phẳng (P), đường thẳng d nằm trong mặt phẳng (P). Quan sát Hình 27 và cho biết:
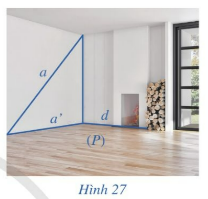
a) Nếu đường thẳng d vuông góc với hình chiếu a’ thì đường thẳng d có vuông góc với a hay không?
b) Ngược lại, nếu dường thẳng d vuông góc với a thì đường thẳng d có vuông góc với hình chiếu a’ hay không

Quan sát hình vẽ để trả lời

Gọi A, B là 2 điểm phân biệt thuộc a
Gọi A’, B’ lần lượt là hình chiếu của A và B trên (P)
a) Vì \(d \subset \left( P \right)\) nên \(d \bot AA’\)
Vậy nếu \(d \bot a’\) thì \(d \bot mp\left( {a,a’} \right)\) do đó \(d \bot a\)
b) Ngược lại, nếu \(d \bot a\) thì \(d \bot mp\left( {a,a’} \right)\) do đó \(d \bot a’\)
Luyện tập - vận dụng 7
Advertisements (Quảng cáo)
Cho hình chóp S.ABCD có \(SA \bot (ABCD)\) và đáy ABCD là hình chữ nhật. Chứng minh rằng các tam giác SBC và SCD là các tam giác vuông

Để chứng minh một tam giác là tam giác vuông ta chứng minh tam giác đó có một góc bằng 90o. Hoặc chứng minh tam giác có 2 cạnh vuông góc với nhau.

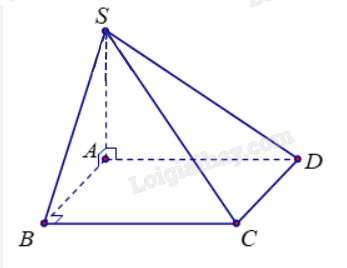
Vì ABCD là hình chữ nhật nên \(BC \bot AB\).
Vì \(SA \bot (ABCD) \Rightarrow SA \bot AB,\,SA \bot CD\)
+ Ta có:
\(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\\AB \cap SA = A\\AB,\,SA \subset (SAB)\end{array} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot SB\)
Xét \(\Delta SBC\) có \(BC \bot SB \Rightarrow \)Tam giác SBC vuông tại B.
+ Ta có:
\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\\AD \cap SA = A\\AD,\,SA \subset (SAD)\end{array} \right. \Rightarrow CD \bot (SAD) \Rightarrow CD \bot SD\)
Xét \(\Delta SCD\) có \(CD \bot SD \Rightarrow \)Tam giác SCD vuông tại D.
