
Chọn ngẫu nhiên 2 đỉnh của một hình bát giác đều nội tiếp trong đường tròn tâm \(O\) bán kính \(R\). Xác suất để khoảng cách giữa hai đỉnh đó bằng \(R\sqrt 2 \) là
A. \(\frac{2}{7}\).
B. \(\frac{3}{7}\).
C. \(\frac{4}{7}\).
D. \(\frac{5}{{56}}\).

Sử dụng công thức tính xác suất: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Advertisements (Quảng cáo)

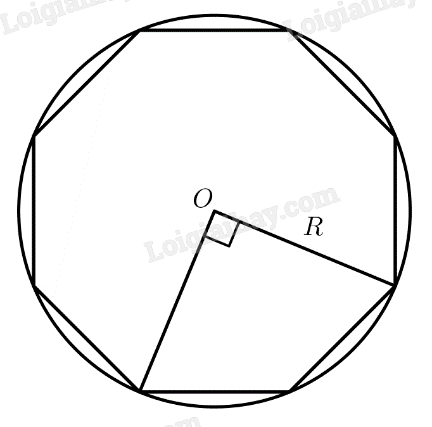
\(A\) là biến cố “Khoảng cách giữa hai đỉnh đó bằng \(R\sqrt 2 \)”
Chọn ngẫu nhiên 2 đỉnh trong tổng số 8 đỉnh có \({C}_8^2 = 28\) cách \( \Rightarrow n\left( \Omega \right) = 28\)
Để khoảng cách 2 đỉnh bằng \(R\sqrt 2 \) thì 2 đỉnh cách nhau 1 đỉnh. Vậy có 8 cách \( \Rightarrow n\left( A \right) = 8\)
\( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{8}{{28}} = \frac{2}{7}\)
Chọn A.
