Chứng minh đường thẳng a không thuộc (P) song song với mặt phẳng (P). Giải và trình bày phương pháp giải - Bài 4.13 trang 105 SGK Toán 11 tập 1 - Cùng khám phá - Bài 3. Đường thẳng và mặt phẳng song song. Cho tứ diện ABCD. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC, ACD. Chứng minh rằng đường thẳng GG’ song song với hai mặt phẳng (ABD) và (BCD)...

Cho tứ diện ABCD. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC, ACD. Chứng minh rằng đường thẳng GG’ song song với hai mặt phẳng (ABD) và (BCD).

Chứng minh đường thẳng a không thuộc (P) song song với mặt phẳng (P):
+ Tìm đường thẳng b thuộc (P) sao cho a // b.
+ Suy ra a // (P).
Advertisements (Quảng cáo)

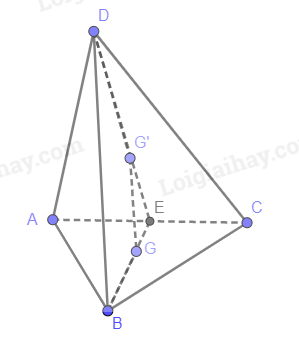
Gọi E là trung điểm AC
\( \Rightarrow EG = \frac{1}{3}BE,EG’ = \frac{1}{3}DE\)
Xét tam giác EDB có \(\frac{{EG}}{{BE}} = \frac{{EG’}}{{DE}} = \frac{1}{3}\) nên GG’ // BD
Suy ra GG’ // (BCD), GG’ // (BCD).
