
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.
a) Gọi O và O’ lần lượt là tâm của các hình bình hành ABCD và ABEF. Chứng minh rằng đường thẳng OO’ song song với các mặt phẳng (ADF) và (BCE).
b) Gọi M và N lần lượt là trọng tâm của hai tam giác ABD và ABE. Chứng minh rằng đường thẳng MN song song với mặt phẳng (CEF).

Chứng minh đường thẳng a không thuộc (P) song song với mặt phẳng (P):
+ Tìm đường thẳng b thuộc (P) sao cho a // b.
+ Suy ra a // (P).

a,
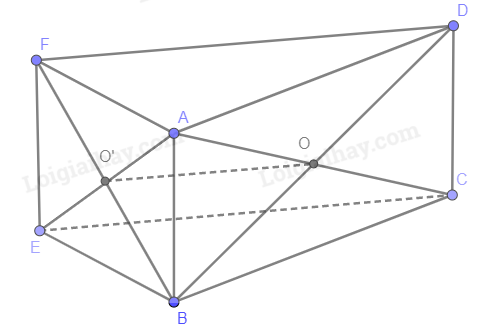
O, O’ lần lượt là tâm hình bình hành ABCD và ABEF nên O là trung điểm AC và BD, O’ là trung điểm AE và BF (Tính chất hình bình hành)
Advertisements (Quảng cáo)
Xét tam giác BFD có O là trung điểm BD, O’ là trung điểm BF nên OO’ là đường trung bình. Suy ra OO’ // FD
Nên OO’ // (ADF)
Xét tam giác AEC có O là trung điểm AC, O’ là trung điểm AE nên OO’ là đường trung bình. Suy ra OO’ // CE
Nên OO’ // (BCE).
b)
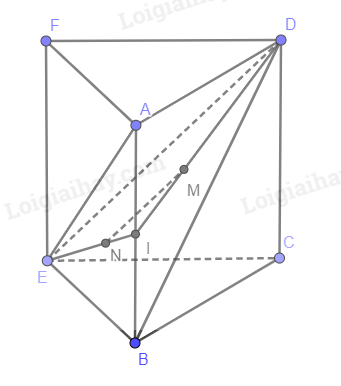
Mở rộng (CEF) thành (CEFD)
Gọi I là trung điểm của AB
M là trọng tâm tam giác ABD nên \(\frac{{IM}}{{ID}} = \frac{1}{3}\)
N là trọng tâm tam giác ABE nên \(\frac{{IN}}{{IE}} = \frac{1}{3}\)
Xét tam giác IDE có \(\frac{{IM}}{{ID}} = \frac{{IN}}{{IE}}\left( { = \frac{1}{3}} \right)\)
Suy ra MN // DE. Mà DE nằm trong (CEFD) nên MN // (CEFD) hay MN // (CEF).
