
Mai tìm hiểu lượng hàm chất béo (đơn vị: g) có trong 100g mỗi loại thực phẩm. Sau khi thu thập dữ liệu về 60 loại thực phẩm, Mai lập được bảng thống kê 5.38.

a) Xác định trung bình, trung bị, mốt của mẫu số liệu.
b) Từ các giá trị tìm được, hãy phân tích số liệu về hàm lượng chất béo của những loại thực phẩm mà Mai đã tìm hiểu.

a)
+) \(\overline x = \frac{1}{N}\left( {{c_1}{n_1} + {c_2}{n_2} + ... + {c_k}{n_k}} \right)\) với \({c_k},{n_k}\) lần lượt là giá trị đại diện và tần số của nhóm thứ k
\({c_k}\) là trung bình cộng của đầu mút trái và đầu mút phải của nhóm đó.
+) Trung vị \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h\) trong đó \({L_m},{n_m},h\) lần lượt là đầu mút trái, tần số và độ dài của nhóm chứa trung vị. \(T\) là tần số tích lũy của nhóm ngay trước nhóm chứa trung vị.
Nhóm chứa trung vị của mẫu số liệu là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{N}{2}\) , trong đó \(N\) là cỡ mẫu.
+) Công thức tìm mốt của mẫu số liệu ghép nhóm là \({M_0} = {L_m} + \frac{a}{{a + b}}.h\)
b) So sánh các giá trị với nhau

+) Tìm trung bình
Advertisements (Quảng cáo)
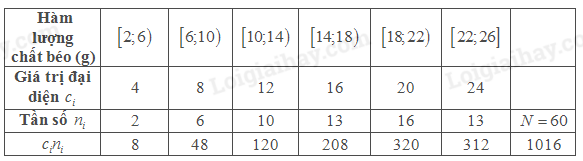
Áp dụng công thức tính trung bình ta có \(\overline x = \frac{{1016}}{{60}} \approx 16,9\)
+ Tìm trung vị
Bảng tần số tích lũy

Ta có \(\frac{N}{2} = \frac{{60}}{2} = 30\). Nhóm có tần số tích lũy lớn hơn bằng 30 là nhóm \(\left[ {14;18} \right)\) nên đây là nhóm chứa trung vị
Ta có \({L_m} = 14;h = 18 - 14 = 4;{n_m} = 13,T = 18\)
Áp dụng công thức tính trung vị ta có \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h = 14 + \frac{{30 - 18}}{{13}}.4 \approx 17,7\)
+ Tìm mốt
Dựa vào bảng tần số ta có nhóm chứa mốt là nhóm \(\left[ {18;22} \right)\) với tần số \(n = 16\)
Ta có \({L_m} = 18;h = 22 - 18 = 4;a = 16 - 13 = 3;b = 16 - 13 = 3\)
Áp dụng công thức tính mốt ta có \({M_0} = {L_m} + \frac{a}{{a + b}}.h = 18 + \frac{3}{{3 + 3}}.4 = 20\)
b) Hàm lượng chất béo trung bình của 60 loại thực phẩm là \(16,9g\)
Hàm lượng chất béo mà Mai tìm hiểu tập chung chủ yếu từ \(17\)g đến \(20\)g
