
Xét mẫu số liệu về lợi nhuận hàng ngày của một cửa hàng trong quãng thời gian 60 ngày
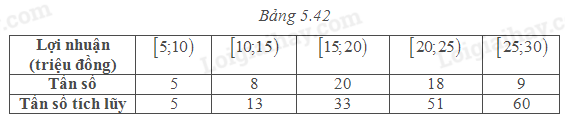
Trong các khẳng định sau, khẳng định nào sai?
A. \({Q_3}\) thuộc nhóm \(\left[ {20;25} \right)\).
B. Nhóm chứa trung vị là nhóm \(\left[ {15;20} \right)\).
C. \({Q_1}\) thuộc nhóm \(\left[ {10;15} \right)\).
D. \({Q_1},{Q_2}\) đều thuộc nhóm \(\left[ {15;20} \right)\).

Advertisements (Quảng cáo)
Nhóm chứa \({Q_i}\left( {i = 1;2;3} \right)\) là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{{iN}}{4}\)
Nhóm chứa trung vị của mẫu số liệu là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{N}{2}\) , trong đó \(N\) là cỡ mẫu.

Đáp án C
* Ta có \(N = 60 \Rightarrow \frac{N}{4} = 15;\frac{N}{2} = 30;\frac{{3N}}{4} = 45\)Ta có \(\frac{N}{2} = \frac{{60}}{2} = 30\).
Từ đó ta xác định được các nhóm chứa \({Q_1};{Q_2};{Q_3}\) lần lượt là \(\left[ {15;20} \right);\left[ {15;20} \right);\left[ {20;25} \right)\)
* Ta có \(\frac{N}{2} = \frac{{60}}{2} = 30\), nên nhóm chứa trung vị là nhóm có tần số tích lũy lớn hơn bằng 30. Vậy nhóm chứa trung vị là nhóm \(\left[ {15;20} \right)\) và đây là \({Q_2}\). Suy ra B đúng
Vậy đáp án đúng là đáp án C
