
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc nhau và SA = SB = SC = a. Khi đó khoảng cách từ S đến mặt phẳng (ABC) bằng
A. \(\frac{a}{{\sqrt 2 }}\)
B. \(\frac{a}{{\sqrt 3 }}\)
C. \(\frac{a}{2}\)
D. \(\frac{a}{3}\)

Tìm đường thẳng đi qua S và vuông góc (ABC)
Advertisements (Quảng cáo)

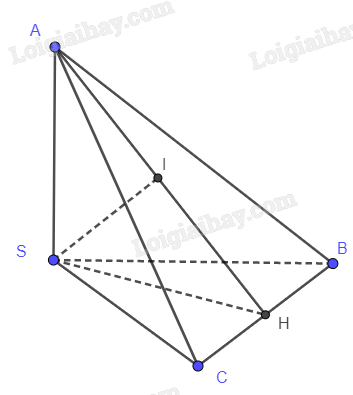
Hạ AH \( \bot \) BC, SI \( \bot \) AH
Ta có: SH \( \bot \) BC, AH \( \bot \) BC suy ra BC \( \bot \) (SAH). Do đó, BC \( \bot \) SI.
Ta có: SI \( \bot \) BC, SI \( \bot \) AH suy ra SI \( \bot \) (ABC)
Suy ra, d(S,(ABC)) = SI
\(\begin{array}{l}BC = \sqrt {S{B^2} + S{C^2}} = \sqrt 2 a\\SH = \frac{{BC}}{2} = \frac{{\sqrt 2 }}{2}a\\\frac{1}{{S{I^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{S{A^2}}} = \frac{1}{{{{\left( {\frac{{\sqrt 2 }}{2}a} \right)}^2}}} + \frac{1}{{{a^2}}}\\ \Leftrightarrow SI = \frac{a}{{\sqrt 3 }}\end{array}\)
Chọn đáp án B.
