
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, BC = 2a, SA vuông góc với mặt phẳng đáy và SA = a.
Khoảng cách giữa hai đường thẳng BD, SC bằng
A. \(\frac{{\sqrt {30} }}{6}a\)
B. \(\frac{{4\sqrt {21} }}{{21}}a\)
C. \(\frac{{2\sqrt {21} }}{{21}}a\)
D. \(\frac{{\sqrt {30} }}{{12}}a\)

Tìm mặt phẳng chứa BD và song song với SC. Sau đó tính khoảng cách.
Advertisements (Quảng cáo)

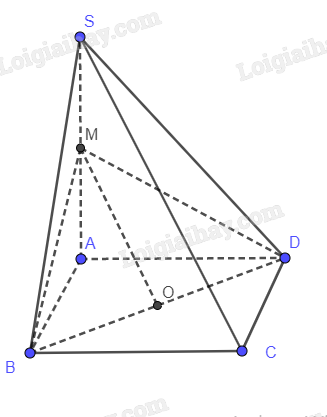
Gọi O là trung điểm BD, M là trung điểm SA
SC // (BMD)
Nên \(d\left( {SC,BD} \right) = d\left( {SC,\left( {BMD} \right)} \right) = d\left( {S,\left( {BMD} \right)} \right) = d\left( {A,\left( {BMD} \right)} \right) = h\)
\(\frac{1}{{{h^2}}} = \frac{1}{{A{M^2}}} + \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} = \frac{1}{{\frac{1}{4}{a^2}}} + \frac{1}{{{a^2}}} + \frac{1}{{4{a^2}}}\)
\( \Rightarrow h = \frac{{2\sqrt {21} a}}{{21}}\)
Chọn đáp án C.
