Hoạt động 1
Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(\Delta \) cắt \(\left( \alpha \right)\). Lấy M là điểm bất kì trong không gian. Qua M, vẽ đường thẳng d song song với \(\Delta \). Hỏi d và \(\left( \alpha \right)\) có điểm chung hay không?

Chứng minh phản chứng (Giả sử d và \(\left( \alpha \right)\) không có điểm chung).

Giả sử d và \(\left( \alpha \right)\) không có điểm chung nên d // \(\left( \alpha \right)\)
\(\Delta \)// d nên \(\Delta \)// \(\left( \alpha \right)\)
Mà \(\Delta \) cắt \(\left( \alpha \right)\) (Mâu thuẫn)
Vậy d và \(\left( \alpha \right)\) có điểm chung.
Luyện tập 1
Cho hình hộp ABCD.A’B’C’D’. Gọi O là giao điểm hai đường chéo AC và BD. Tìm hình chiếu song song của điểm O trên mặt phẳng (A’B’C’D’) theo phương AA’.
Advertisements (Quảng cáo)

Kẻ đường thẳng đi qua O, song song với AA’ và cắt (A’B’C’D’) tại điểm O’. O’ là hình chiếu song song của O.

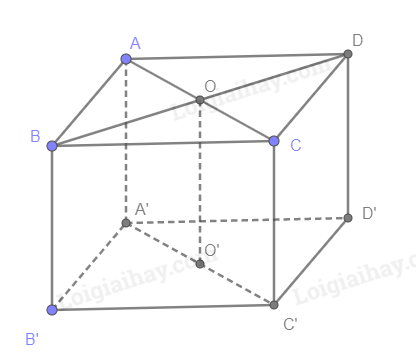
Gọi O’ là trung điểm của A’C’
Do ABCD là hình bình hành, O là giao điểm của AC và BD nên O là trung điểm của AC và BD
Ta có AA’ // CC’ (cùng // BB’) và AA’ = CC’ (cùng = BB’) nên ACC’A’ là hình bình hành
\( \Rightarrow \)OO’ là đường trung bình của hình bình hành ACC’A’ nên OO’ // AA’
Ta lại có OO’ cắt (A’B’C’D’) tại O’
Vậy O’ là hình chiếu song song của O trên mặt phẳng (A’B’C’D’) theo phương AA’.
