Hoạt động 2
Cho hình lăng trụ tam giác ABC.A’B’C’. Lấy M là trung điểm của AB và G là trọng tâm của tam giác ABC. Gọi M’, G’ lần lượt là hình chiếu song song của M và G trên mặt phẳng (A’B’C’) theo phương AA’. Hãy nhận xét về vị trí tương đối của ba điểm M’, G’, C’?

Kẻ đường thẳng đi qua O, song song với AA’ và cắt (A’B’C’D’) tại điểm O’. O’ là hình chiếu song song của O.

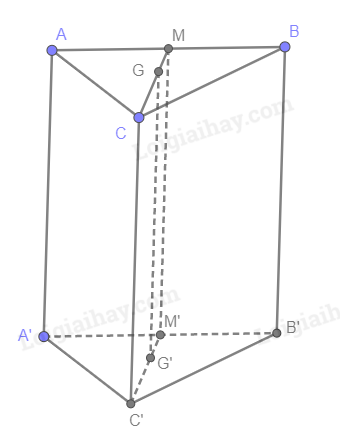
Gọi M’ là trung điểm của A’B’, G’ là trọng tâm của tam giác A’B’C’
Xét hình bình hành ABB’A’ có M, M’ lần lượt là trung điểm của AB, A’B’ nên MM’ // AA’ và CC’ = MM’ (Đường trung bình của hình bình hành)
MM’ cắt (A’B’C’) tại M’ nên M’ là hình chiếu song song của M trên (A’B’C’) theo phương AA’
Ta có: CC’ // MM’ (cùng // AA’) và CC’ = MM’ (cùng = AA’) nên CC’M’M là hình bình hành. Suy ra CM // C’M’ (1) và CM = C’M’
\(CG = \frac{2}{3}CM,C’G’ = \frac{2}{3}C’M’ \Rightarrow CG = C’G’\) (2)
Từ (1), (2) suy ra CGG’C’ là hình bình hành \( \Rightarrow \)CC’ // GG’ \( \Rightarrow {\rm{AA’}}\,{\rm{//}}\,{\rm{GG’}}\)
GG’ cắt (A’B’C’) tại G’ nên G’ là hình chiếu song song của G trên (A’B’C’) theo phương AA’
Ba điểm M’, G’, C’ thẳng hàng.
Luyện tập 2
Advertisements (Quảng cáo)
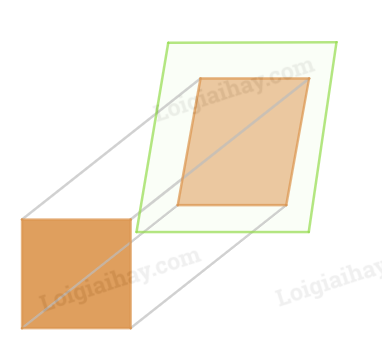
a) Hình chiếu song song của một hình vuông có thể là hình bình hành không? Hãy cho một ví dụ minh hoạ.
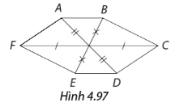
b) Hình 4.97 có thể là hình chiếu song song của hình lục giác đều được không? Vì sao?

a) Hình chiếu song song của một hình vuông có thể là hình bình hành.
b) Phép chiếu song song biến 2 đường thẳng song song thành 2 đường thẳng song song hoặc trùng nhau.

a) Hình chiếu song song của một hình vuông có thể là hình bình hành. Ví dụ:
b)
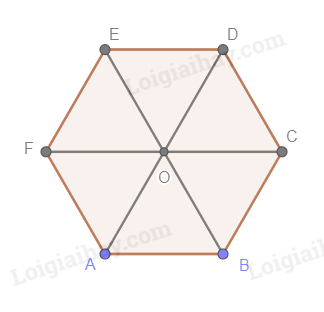
Gọi O là giao điểm của các đường chéo của lục giác đều ABCDEF
Hình 4.97 không thể là hình chiếu song song của hình lục giác đều vì:
Ta có: AO // BC
Phép chiếu song song biến 2 đường thẳng song song thành 2 đường thẳng song song hoặc trùng nhau. Mà Hình 4.97 không thể hiện được điều đó.
