Hình hộp ABCD.A’B’C’D’ có AB = AA’ = AD = a và . Câu 12 trang 124 SGK Hình học 11 Nâng cao - Các câu hỏi trắc nghiệm
Hình hộp ABCD.A’B’C’D’ có AB = AA’ = AD = a và \(\widehat {A’AB} = \widehat {A’AD} = \widehat {BAD} = 60^\circ .\) Khi đó, khoảng cách giữa các đường thẳng chứa các cạnh đối diện của tứ diện AA’BD bằng :
A. \({{a\sqrt 2 } \over 2}\)
B. \({{a\sqrt 3 } \over 2}\)
C. \(a\sqrt 2 \)
D. \({{3a} \over 2}\)
Advertisements (Quảng cáo)
Chọn (A)
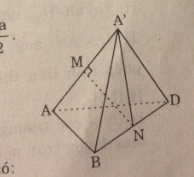
Tứ diện A’ABD là tứ diện đều cạnh a.
M, N lần lượt là trung điểm AA’, BD.
MN là đoạn vuông góc chung của AA’ và BD. Ta có:
\(M{N^2} = A'{N^2} - A'{M^2} = {\left( {{{a\sqrt 3 } \over 2}} \right)^2} - {\left( {{a \over 2}} \right)^2} = {{3{a^2}} \over 4} - {{{a^2}} \over 4} = {{{a^2}} \over 2} \Rightarrow {\rm M}{\rm N} = {{a\sqrt 2 } \over 2}\)