Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD). Hai điểm M và N lần lượt thay đổi trên cạnh CB và CD, đặt CM =x, CN = y. Tìm hệ thức liên hệ giữa x và y để :
a. Hai mặt phẳng (SAM) và (SAN) tạo với nhau góc 45˚ ;
b. Hai mặt phẳng (SAM) và (SMN) vuông góc với nhau.

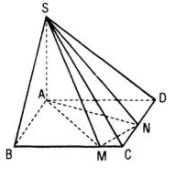
a. Ta có: AM, AN cùng vuông góc với SA mà \(\widehat {MAN} \le 90^\circ \) nên \(\widehat {MAN}\) là góc giữa hai mặt phẳng (SAM) và (SAN). Hai mặt phẳng đó tạo với nhau góc 45˚ khi và chỉ khi \(\widehat {MAN} = 45^\circ \)
Mặt khác, M ϵ BC, N ϵ CD, \(\widehat {BAD} = 90^\circ \) nên điều
đó xảy ra khi \(\widehat {BAM} + \widehat {DAN} = 45^\circ ,\)
Advertisements (Quảng cáo)
Từ đó ta có : \(1 = {{\tan \widehat {BAM} + \tan \widehat {DAN}} \over {1 - \tan \widehat {BAM}.\tan \widehat {DAN}}}\,\,\left( * \right)\)
(Áp dụng công thức \(\tan \left( {x + y} \right) = {{\tan x + \tan y} \over {1 - \tan x\tan y}}\) )
Vì \(\tan \widehat {BAM} = {{a - x} \over a},\tan \widehat {DAN} = {{a - y} \over a},\) nên \(\left( * \right) \Leftrightarrow 2{a^2} + xy = 2a\left( {x + y} \right)\)
Đó là hệ thức liên hệ giữa x và y để các mặt phẳng (SAM) và (SAN) tạo với nhau góc 45˚
b. Ta có: (SAM) ⊥ (ABCD), từ đó nếu (SMN) ⊥ (SAM) thì giao tuyến MN của (SMN) và (ABCD) sẽ vuông góc với (SAM), tức MN ⊥ AM.
Ngược lại, nếu có MN ⊥ AM thì do SA ⊥ MN nên MN ⊥ (SAM), suy ra (SMN) ⊥ (SAM)
Vậy (SAM) ⊥ (SMN) khi và chỉ khi \(\widehat {AMN} = 90^\circ .\)
\(\eqalign{ & \Leftrightarrow {a^2} + {\left( {a - x} \right)^2} + {x^2} + {y^2} = {a^2} + {\left( {a - y} \right)^2} \cr & \Leftrightarrow ay = x\left( {a - x} \right) \text{ với } 0 \le x \le a,0 \le y \le a. \cr} \)
