Tam giác ABC vuông có cạnh huyền BC nằm trong mp(P), cạnh AB và AC lần lượt tạo với mp(P) các góc β và γ. Gọi α là góc tạo bởi mp(P) và mp(ABC). Chứng minh rằng . Câu 4 trang 120 SGK Hình học 11 Nâng cao - Bài tập ôn tập chương III
Tam giác ABC vuông có cạnh huyền BC nằm trong mp(P), cạnh AB và AC lần lượt tạo với mp(P) các góc β và γ. Gọi α là góc tạo bởi mp(P) và mp(ABC). Chứng minh rằng \({\sin ^2}\alpha = {\sin ^2}\beta + {\sin ^2}\gamma \)
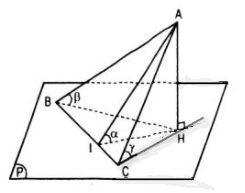
Kẻ AH ⊥ mp(P) và AI ⊥ BC
Advertisements (Quảng cáo)
Thì \(\beta = \widehat {ABH},\gamma = \widehat {ACH},\alpha = \widehat {AIH}.\)
Vì ΔABC vuông ở A nên :
\(\eqalign{ & {1 \over {A{I^2}}} = {1 \over {A{B^2}}} + {1 \over {A{C^2}}} \cr & \Rightarrow {{A{H^2}} \over {A{I^2}}} = {{A{H^2}} \over {A{B^2}}} + {{A{H^2}} \over {A{C^2}}} \cr & hay\,\,{\sin ^2}\alpha = {\sin ^2}\beta + {\sin ^2}\gamma \cr} \)