Bài 6. Gọi F là phép biến hình có tính chất sau đây: Với mọi cặp điểm M, N và ảnh M’, N’ của chúng, ta luôn có \(\overrightarrow {M’N’} = k\overrightarrow {MN} \) , trong đó k là một số không đổi khác 0. Hãy chứng minh rằng F là phép tịnh tiến hoặc phép vị tự

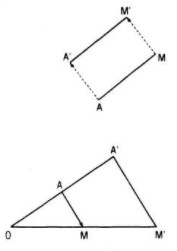
Ta lấy một điểm A cố định và đặt A’ = F(A)
Theo giả thiết, với điểm M bất kì và ảnh M’ =F(M) của nó, ta có \(\overrightarrow {A’M} = k\overrightarrow {AM} \)
Nếu k = 1, thì \(\overrightarrow {A’M’} = \overrightarrow {AM} \), do đó \(\overrightarrow {MM’} =\overrightarrow {AA’} \) ,và F là phép tịnh tiến theo vecto \(\overrightarrow {AA’} \)
Advertisements (Quảng cáo)
Nếu k ≠ 1 thì có điểm O sao cho:
\(\overrightarrow {OA’} = k\overrightarrow {OA} \) (với O thỏa \(\overrightarrow {OA} = {1 \over {1 - k}}\overrightarrow {AA’} \) )
Khi đó ta có:
\(\overrightarrow {OM’} = \overrightarrow {OA’} + \overrightarrow {A’M’} = k\overrightarrow {OA} + k\overrightarrow {AM} = k\overrightarrow {OM} \)
Vậy F là phép vị tự tâm O, tỉ số k
