Cho hình chóp S.ABC. Gọi K và N lần lượt là trung điểm của SA và BC ; M là điểm nằm giữa S và C.
a. Chứng minh rằng mặt phẳng đi qua K, song song với AB và SC thì đi qua điểm N.
b. Xác định thiết diện của hình chóp S.ABC khi cắt bởi mp(KMN). Chứng tỏ rằng KN chia thiết diện thành hai phần có diện tích bằng nhau.

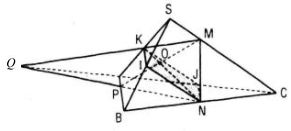
a. Gọi I và J lần lượt là trung điểm của SB và AC thì dễ thấy các điểm K, I, N, J cùng thuộc mặt phẳng song song với AB và SC. Vậy mặt phẳng đi qua K, song song với AB và SC thì đi qua điểm N.
Advertisements (Quảng cáo)
b. Nếu M là trung điểm của SC thì thiết diện của hình chóp S.ABC khi cắt bởi mp(MKN) là hình bình hành, trong đó P là trung điểm của AB. Khi đó KN chia hình bình hành MKPN thành hai phần có diện tích bằng nhau. Nếu M không là trung điểm của SC. Gọi Q là giao điểm của KM và AC, P là giao điểm của QN và AB. Khi đó thiết diện của hình chóp S.ABC cắt bởi mp(MKN) là tứ giác MKPN.
Ta có: SC // (α) và AB // (α), đồng thời K là trung điểm SA nên : d(M, (α)) = d(P, (α))
⇒ OP = OM (với O là giao điểm của PM và NK)
Do đó hai đường cao của hai tam giác MKN và PKN kẻ từ M và P bằng nhau,
Từ đó suy ra \({S_{PKN}} = {S_{MKN}}\)
