Câu 4 trang 126 SGK Hình học 11: ÔN TẬP CUỐI NĂM - HÌNH HỌC 11. Cho hình lăng trụ tứ giác ABCD.A’B’C’D’ có E, F, M và N lần lượt là trung điểm của AC, BD, AC’ và BD’. Chứng minh MN = EF.
Bài 4. Cho hình lăng trụ tứ giác \(ABCD.A’B’C’D’\) có \(E, F, M\) và \(N\) lần lượt là trung điểm của \(AC, BD, AC’\) và \(BD’\). Chứng minh \(MN = EF\).

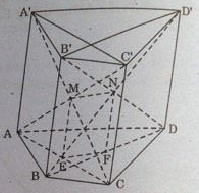
Vì \(M\) là trung điểm của \(A’C\) và \(E\) là trung điểm của \(AC\) nên
Advertisements (Quảng cáo)
\(\overrightarrow {EM} = {1 \over 2}\overrightarrow {AA’} (1)\)
Tương tự ta có: \(\overrightarrow {FN} = {1 \over 2}\overrightarrow {BB’} (2)\)
Ta lại có: \(\overrightarrow {AA’} = \overrightarrow {BB’} (3)\)
Từ (1), (2), (3) ⇒ \(\overrightarrow {EM} = \overrightarrow {FN}\) hay tứ giác \(EFNM\) là hình bình hành, do đó \(MN = EF\).
