Bài 6. Cho hình lập phương \(ABCD.A’B’C’D’\) có cạnh bằng \(a\).
a) Hãy xác định đường vuông góc chung của hai đường thẳng chéo nhau \(BD’\) và \(B’C\).
b)Tính khoảng cách của hai đường thẳng \(BD’\) và \(B’C\)

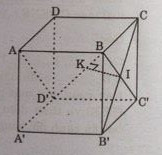
a) \(AB ⊥ (BCC’B’) ⇒ AB ⊥ B’C\)
\(BCC’B’\) là hình vuông có \(BC’ ⊥ B’C\)
Advertisements (Quảng cáo)
\(⇒ B’C ⊥ (ABC’D’)\) và \(BD’ ⊂ (ABC’D’)\)
Trong mặt phẳng \((ABC’D’)\) ta kẻ \(IK ⊥ BD’\) vì \(B’C ⊥ (ABC’D’) ⇒ B’C ⊥ IK\)
Kết hợp với \(IK ⊥ BD’ ⇒ IK\) là đường vuông góc chung của \(B’C\) và \(BD’\)
b) Ta tính \(IK\) từ hình chữ nhật \(ABC’D’\) với \(AB = a, BC’ = a\sqrt2, BD’ = a\sqrt3\)
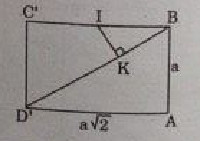
\(∆BIK\) đồng dạng \(∆BD’C’\) ta có:
\(\eqalign{
& \Rightarrow {{IK} \over {D’C’}} = {{BI} \over {B{\rm{D}}’}} \cr
& \Rightarrow IK = {{BI.D’C’} \over {B{\rm{D}}’}} \cr
& IK = {1 \over 6}a\sqrt 6 \cr} \).
