
Doanh thu theo tháng của một cửa hàng trong hai năm 2022 và 2023 được cho như sau:
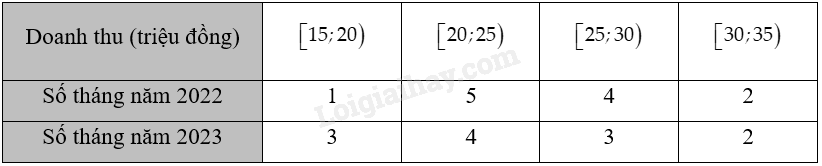
Tính độ lệch chuẩn của hai mẫu số liệu ghép nhóm và cho biết trong năm nào cửa hàng này có doanh thu hằng tháng ổn định hơn.

Chọn giá trị đại diện cho các nhóm số liệu, xét từng mẫu số liệu, tính cỡ mẫu, giá trị trung
bình và độ lệch chuẩn theo các công thức đã học. So sánh hai giá trị độ lệch chuẩn vừa
tìm được để nhận xét về sự ổn định doanh thu hằng tháng của mỗi năm.

Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:
Advertisements (Quảng cáo)
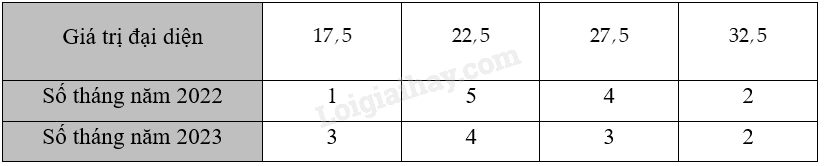
+ Xét mẫu số liệu doanh thu trong năm 2022:
Cỡ mẫu là \(n = 1 + 5 + 4 + 2 = 12\).
Doanh thu trung bình mỗi tháng là \(\overline x = \frac{1}{{12}}\left( {1 \cdot 17,5 + 5 \cdot 22,5 + 4 \cdot 27,5 + 2 \cdot 32,5} \right) = \frac{{305}}{{12}}\).
Độ lệch chuẩn là \({s_{2022}} = \sqrt {\frac{1}{{12}}\left( {1 \cdot {{17,5}^2} + 5 \cdot {{22,5}^2} + 4 \cdot {{27,5}^2} + 2 \cdot {{32,5}^2}} \right) - {{\left( {\frac{{305}}{{12}}} \right)}^2}} = \frac{{5\sqrt {107} }}{{12}} \approx 4,31\).
+ Xét mẫu số liệu doanh thu trong năm 2023:
Cỡ mẫu là \(n = 3 + 4 + 3 + 2 = 12\).
Doanh thu trung bình mỗi tháng là \(\overline x = \frac{1}{{12}}\left( {3 \cdot 17,5 + 4 \cdot 22,5 + 3 \cdot 27,5 + 2 \cdot 32,5} \right) = \frac{{145}}{6}\).
Độ lệch chuẩn là \({s_{2023}} = \sqrt {\frac{1}{{12}}\left( {3 \cdot {{17,5}^2} + 4 \cdot {{22,5}^2} + 3 \cdot {{27,5}^2} + 2 \cdot {{32,5}^2}} \right) - {{\left( {\frac{{145}}{6}} \right)}^2}} = \frac{{5\sqrt {38} }}{6} \approx 5,14\).
Do \({s_{2022}}
