
Lợi nhuận của 20 nhà đầu tư quy mô nhỏ ở hai lĩnh vực A và B được cho như sau (lợi nhuận âm được hiểu là lỗ vốn):
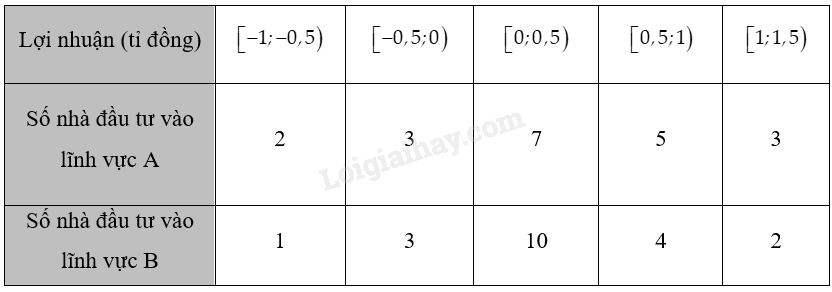
Hỏi đầu tư vào lĩnh vực nào “rủi ro” hơn?

Tính độ lệch của hai mẫu số liệu ghép nhóm, so sánh độ lệch chuẩn của từng lĩnh vực, lĩnh vực có độ lệch chuẩn lớn hơn sẽ có độ rủi ro lớn hơn khi đầu tư.

Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:
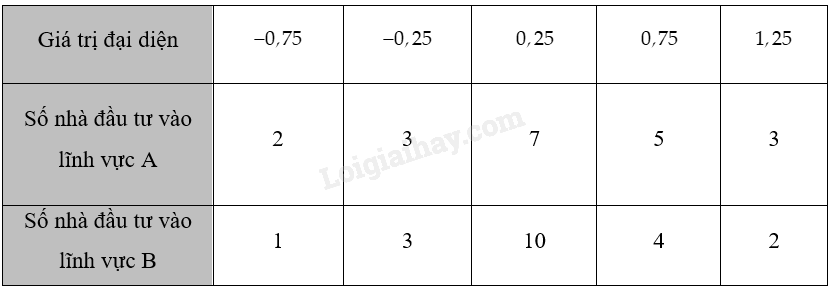
+ Xét mẫu số liệu lợi nhuận của lĩnh vực A
Cỡ mẫu là \(n = 1 + 3 + 10 + 4 + 2 = 20\).
Advertisements (Quảng cáo)
Lợi nhuận trung bình của mỗi nhà đầu tư là
\(\overline x = \frac{1}{{20}}\left[ {2 \cdot \left( { - 0,75} \right) + 3 \cdot \left( { - 0,25} \right) + 7 \cdot 0,25 + 5 \cdot 0,75 + 3 \cdot 1,25} \right] = \frac{7}{{20}} = 0,35\).
Độ lệch chuẩn là
\({s_A} = \sqrt {\frac{1}{{20}}\left[ {2 \cdot {{\left( { - 0,75} \right)}^2} + 3 \cdot {{\left( { - 0,25} \right)}^2} + 7 \cdot {{0,25}^2} + 5 \cdot {{0,75}^2} + 3 \cdot {{1,25}^2}} \right] - {{0,35}^2}} = \frac{{\sqrt {34} }}{{10}} \approx 0,58\).
+ Xét mẫu số liệu lợi nhuận của lĩnh vực B
Cỡ mẫu là \(n = 2 + 3 + 7 + 5 + 3 = 20\).
Lợi nhuận trung bình của mỗi nhà đầu tư là
\(\overline x = \frac{1}{{20}}\left[ {1 \cdot \left( { - 0,75} \right) + 3 \cdot \left( { - 0,25} \right) + 10 \cdot 0,25 + 4 \cdot 0,75 + 2 \cdot 1,25} \right] = \frac{{13}}{{40}} = 0,325\).
Độ lệch chuẩn là
\({s_B} = \sqrt {\frac{1}{{20}}\left[ {1 \cdot {{\left( { - 0,75} \right)}^2} + 3 \cdot {{\left( { - 0,25} \right)}^2} + 10 \cdot {{0,25}^2} + 4 \cdot {{0,75}^2} + 2 \cdot {{1,25}^2}} \right] - {{0,325}^2}} = \frac{{\sqrt 5 }}{{20}} \approx 0,11\).
Suy ra \({s_A} > {s_B}\). Vậy đầu tư vào lĩnh vực A “rủi ro” hơn lĩnh vực B.
