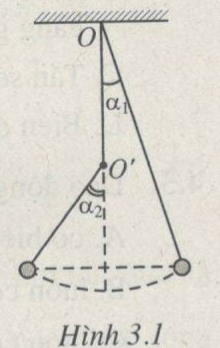
3.15. Một con lắc đơn dài 1,0 m. Phía dưới điểm treo O trên phương thẳng đứng có một chiếc đinh đóng chắc vào điểm O’ cách O một đoạn OO’ = 0,5 m, sao cho con lắc vấp vào đinh khi dao động (H.3.1). Kéo con lắc lệch khỏi phương thẳng đứng một góc \(\alpha\)1 =10° rồi thả không vận tốc đầu. Bỏ qua ma sát. Hãy tính :
a) Biên độ góc của con lắc ở hai bên vị trí cân bằng.
b) Chu kì dao động của con lắc. Lấy g = 9,8 m/s2. Hình 3.1
Hướng dẫn giải chi tiết
a) Biên độ góc của con lắc ở hai bên vị trí cân bằng.
Advertisements (Quảng cáo)
Theo định luật bảo toàn năng lượng ta suy ra hai vị trí biên phải ở cùng 1 độ cao (H3.1.G)
\(\eqalign{
& {h_A} = {h_B}l \cr
& (1 - \cos {\alpha _1}) = {l \over 2}(1 - \cos {\alpha _2}) \cr
& \Rightarrow \cos {\alpha _2} = 2\cos {\alpha _1} - 1 \cr
& = 2\cos {10^0} - 1 = 0,9696 \cr
& \Rightarrow {\alpha _0} = {14^0} \cr}\)
b) Chu kì dao động của con lắc
\(\eqalign{
& T = {{{T_1} - {T_2}} \over 2};\,\,{T_1} = 2\pi \sqrt {{l \over g}} {\mkern 1mu} ;\,\,{T_2} = 2\pi \sqrt {{l \over {2g}}} \cr
& T = 2\pi \sqrt {{l \over g}} \left( {1 + {1 \over {\sqrt 2 }}} \right) \cr
& = 3,14\sqrt {{1 \over {9,8}}} \left( {1 + {1 \over {\sqrt 2 }}} \right) = 1,7s \cr} \)
