
Bảng 19, Bảng 20 lần lượt biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của hai công ty A, B (đơn vị: triệu đồng)
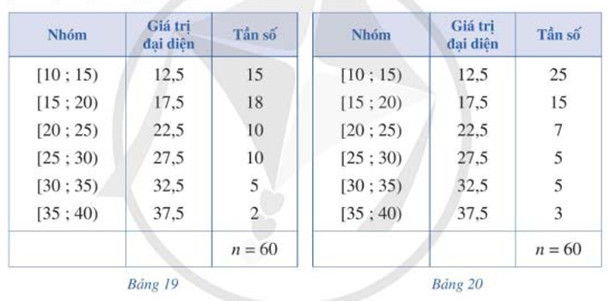
a) Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm lần lượt biểu diễn mức lương của hai công ty A,B
b) Công ty nào có mức lương đồng đều hơn?

a) \({s^2} = \frac{{{n_1}.{{({x_1} - \overline x )}^2} + {n_2}{{({x_2} - \overline x )}^2} + ... + {n_p}{{({x_p} - \overline x )}^2}}}{n}\)
\(s = \sqrt {{s^2}} \)
b) Công ty nào có độ lệch chuẩn nhỏ hơn thì có mức lương đồng đều hơn
Advertisements (Quảng cáo)

Số trung bình cộng của mẫu số liệu ghép nhóm của công ty A là: \(\overline {{x_A}} = \frac{{15.12,5 + 18.17,5 + 10.22,5 + 10.27,5 + 5.32,5 + 2.37,5}}{{60}} = \frac{{62}}{3}\)
Phương sai của mẫu số liệu ghép nhóm của công ty A là:
\({s_A}^2 = \frac{{15.{{(12,5 - \frac{{62}}{3})}^2} + 18.{{(17,5 - \frac{{62}}{3})}^2} + 10.{{(22,5 - \frac{{62}}{3})}^2} + 10.{{(27,5 - \frac{{62}}{3})}^2} + 5.{{(32,5 - \frac{{62}}{3})}^2} + 2.{{(37,5 - \frac{{62}}{3})}^2}}}{{60}} \approx 49,14\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm của công ty A là: \({s_A} = \sqrt {{s_A}^2} = \sqrt {49,13} \approx 7\)
Số trung bình cộng của mẫu số liệu ghép nhóm của công ty B là: \(\overline {{x_B}} = \frac{{25.12,5 + 15.17,5 + 7.22,5 + 5.27,5 + 5.32,5 + 3.37,5}}{{60}} = \frac{{229}}{{12}}\)
Phương sai của mẫu số liệu ghép nhóm của công ty B là:
\(\begin{array}{l}{s_B}^2 = \frac{{25.{{(12,5 - \frac{{229}}{{12}})}^2} + 15.{{(17,5 - \frac{{229}}{{12}})}^2} + 7.{{(22,5 - \frac{{229}}{{12}})}^2} + 5.{{(27,5 - \frac{{229}}{{12}})}^2} + 5.{{(32,5 - \frac{{229}}{{12}})}^2} + 3.{{(37,5 - \frac{{229}}{{12}})}^2}}}{{60}}\\ \approx 57,91\end{array}\)Độ lệch chuẩn của mẫu số liệu ghép nhóm của công ty B là: \({s_B} = \sqrt {{s_B}^2} = \sqrt {57,91} \approx 7,61\)
Nhận thấy độ lệch chuẩn của công ty A nhỏ hơn công ty B nên mức lương của công ty A đồng đều hơn
