Câu hỏi/bài tập:

Cho khối tròn xoay như Hình 39
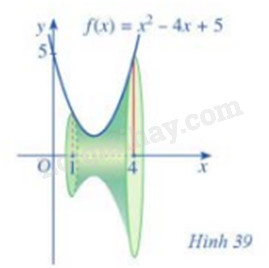
a) Hình phẳng được giới hạn bởi các đường nào để khi quay quanh trục Ox ta được khối tròn xoay như Hình 39
b) Tính thể tích khối tròn xoay đó
Advertisements (Quảng cáo)

a) Quan sát hình vẽ
b) Cho hàm số y = f(x) liên tục, không âm trên đoạn [a;b]. Hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b quay quanh trục Ox tạo thành một khối tròn xoay có thể tích bằng \(V = \pi \int\limits_a^b {{{[f(x)]}^2}dx} \)

a) Hình phẳng được giới hạn bởi đồ thị hàm số \(f(x) = {x^2} - 4x + 5\), trục Ox, hai đường thẳng x = 1 và x = 4 để khi quay quanh trục Ox ta được khối tròn xoay như Hình 39
b) Thể tích khối tròn xoay đó là: \(V = \pi \int\limits_1^4 {{f^2}(x)} dx = \int\limits_1^4 {{{\left( {{x^2} - 4x + 5} \right)}^2}dx} = \frac{{78}}{5}\)
