Câu hỏi/bài tập:

Một khinh khí cầu bay với độ cao (so với mực nước biển) tại thời điểm t là h(t), trong đó t tính bằng phút, h(t) tính bằng mét. Tốc độ bay của khinh khí cầu được cho bởi hàm số \(v(t) = - 0,12{t^2} + 1,2t\) với t tính bằng phút, v(t) tính bằng mét/ phút. Tại thời điểm xuất phát (t=0), khinh khí cầu ở độ cao 520m và 5 phút sau khi xuất phát (t = 0), khinh khí cầu ở độ cao 520m và 5 phút sau khi xuất phát, khinh khí cầu đã ở độ cao 530m
a) Viết công thức xác định hàm số h(t) \((0 \le t \le 29)\)
b) Độ cao tối đa của khinh khí cầu khi bay là bao nhiêu?
c) Khi nào khinh khí cầu sẽ trở lại độ cao khi xuất phát?

a) \(h(t) = \int {v(t)} dt\)
b) Khảo sát hàm số h(t)
c) Giải phương trình

Advertisements (Quảng cáo)
a) \(h(t) = \int {v(t)} dt = \int {\left( { - 0,12{t^2} + 1,2t} \right)dt} = - 0,04{t^3} + 0,6{t^2} + C\)
Tại t = 0 thì h(0) = 520 => C = 520
Vậy \(h(t) = - 0,04{t^3} + 0,6{t^2} + 520\)
b) Xét \(h(t) = - 0,04{t^3} + 0,6{t^2} + 520\)
\(h'(t) = v(t) = - 0,12{t^2} + 1,2t \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 10\end{array} \right.\)
Bảng biến thiên:
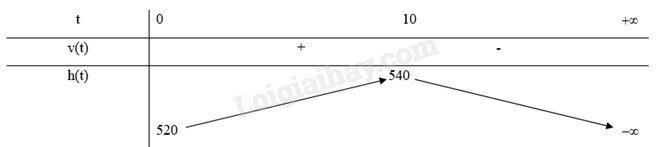
Từ bảng biến thiên, ta thấy độ cao tối đa của khinh khí cầu khi bay là 540m
c) Khinh khí cầu trở lại độ cao xuất phát khi:
\(h(t) = - 0,04{t^3} + 0,6{t^2} + 520 = 520 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 15\end{array} \right.\)
Vậy sau 15 phút thì khinh khí cầu trở lại độ cao xuất phát
